清華大學建筑學院建筑節能研究中心   卜凡  燕 達  孫紅三

       【摘  要】建筑表面的輻射得熱是影響建筑運行能耗的重要因素之一，這其中主要包括太陽輻射得熱和長波輻射得熱。因此，控制建筑表面對輻射的吸收/發射是降低建筑運行能耗的重要技術手段。光譜選擇性輻射制冷膜通過以高反射率反射絕大部分太陽輻射并選擇性吸收和發射長波輻射來實現長波輻射散熱，實現物體表面全天散熱。隨著材料制備技術發展，實驗室中已經實現這類輻射制冷材料的制備并可大規模生產。為研究這類材料在建筑上的應用潛力，需要在光譜尺度下對輻射換熱進行建模計算并與建筑性能模擬耦合，實現這類材料在建筑上應用的模擬計算。然而，由于以光譜尺度的積分在單位時間步長下的計算時間長，因此在計算大型建筑多個表面的輻射換熱時，計算代價增長較快。本研究基于分段積分、多元回歸分析和神經網絡算法，對光譜計算結果進行了擬合和模型重建，提出了能夠大幅降低輻射膜計算時間的簡化方法，并保證了一定的計算精度。

       【關鍵詞】建筑性能模擬；輻射制冷膜；回歸分析；神經網絡

0 引言

       建筑用能占全社會用能的比例接近20%，隨著城鎮化率的進一步提高和人民生活水平的日益增長，建筑用能仍然在未來一段時間內有增長趨勢。在建筑能耗中，制冷是能源消耗的重要部分。在各項建筑用能中，制冷能耗的增長速度較高，自2000年起，就以13%的年增長率高速增長。因此，高效制冷是降低建筑能耗、實現建筑節能的重要途徑之一^[1]。

       建筑表面的輻射得熱是影響建筑需冷量和需熱量的重要影響因素之一。輻射得熱包括太陽輻射和長波輻射兩個部分。太陽輻射主要受日照時刻和大氣云量的影響，在日間造成建筑表面的得熱。長波輻射主要存在于建筑表面與大氣之間，由于大氣在白天極易被加熱，此時長波輻射造成建筑表面的得熱，而在夜間，大氣降溫至零下數十度，此時建筑通過表面與大氣的長波輻射進行散熱。事實上，由于輻射以光譜尺度進行，大氣并不會全部吸收所有波段的輻射，例如，對于3~5和8~13，大氣幾乎不吸收也不發射這個波段的輻射，而是直接透過，因此這些波段被稱為“大氣窗口”^{[2, 3]}。根據普朗克輻射定律和維恩位移定律^[4]，溫度范圍在0~30的物體表面熱輻射峰值出現在9.6~10.6，恰好位于大氣窗口之間。通過提高大氣窗口內的物體表面發射率，并且降低其他紅外波段的發射率，可以物體表面幾乎不與大氣換熱，而直接將能量輻射至太空中，而微波背景輻射溫度大約為3K[5]。同時，通過增加表面對太陽輻射的反射率，就可以實現全天利用輻射制冷。

       自然界中存在具備這類特殊光譜性質的材料，樹葉上的露水和霜就是通過長波紅外換熱實現表面溫度低于環境露點溫度從而使空氣中的水蒸氣凝結或凝華附著在樹葉表面^[6]。高太陽反射率的例子存在于一種生活在撒哈拉沙漠中的螞蟻，通體銀色，通過特殊的生理結構可以在可見光以及近紅外波段實現接近0.8的反射率，以維持身體溫度在正常水平^[7]。在一些實驗室中，已經實現了對這類材料的人工制備，可以實現在太陽輻射的反射率超過95%，并且實現長波紅外發射率在0.9以上^[8-10]。其中，尹曉波等人制備的材料可具備大規模生產的潛力，具備在建筑上使用的前景。

       在這類采用光譜積分計算輻射制冷膜的研究中，大多是對較短的實驗周期內的研究進行模擬分析。Zhao等人建立了基于積分過程的水循環系統，分析了單位平米能夠通過輻射提供的冷水量^[11]。輻射膜材料測試的研究也多采用3~5天為周期的實驗數據對輻射制冷膜建模來驗證輻射制冷膜的制冷性能^{[8, 12, 13]}。

       然而，在研究輻射膜在建筑上的應用時，現有研究多采用簡化積分過程的方式實現光譜選擇性輻射制冷膜與建筑性能模擬的耦合。Chen和Lu等人通過采用平均發射率的方式簡化光譜選擇性輻射制冷膜在建筑性能模擬中的計算，發現在昆明和香港，一層小型建筑的夏季需冷量分別降低了7.1%和9.3%^[14]。Zhao等人通過回歸方法簡化了積分過程，利用EnergyPlus對一種與屋頂耦合的輻射冷卻系統進行了模擬，得到了0.4~1.5kWh/m²的節能量^[15]。Wang等人同樣利用EnergyPlus^[16]采用二次多項式回歸方法對輻射膜積分過程進行了簡化，對一占地5000平米的三層辦公樓進行了模擬分析^[17]。然而，這種方法缺少對誤差的準確說明，一方面，無法通過對輻射膜本身光譜特性建模來說明輻射膜本身的計算誤差對建筑性能模擬的影響；另一方面，通過平均發射率等方法進行簡化后，可能無法突出光譜選擇性輻射制冷膜對其他材料的優勢，無法全面評估輻射制冷膜的應用潛力。為解決這一問題，Wan，Tan和Yang等人對已有的RTTV模型進行了改進，試圖在RTTV模型中考慮輻射制冷膜帶來的附加換熱系數^{[18, 19]}。然而，盡管這類模型在穩態下能夠有比較好的效果，在夏季往往不能反映建筑本身的動態特性，對耦合模擬的物理過程的刻畫仍然不夠令人滿意。

       本研究，首先通過建立基于光譜積分的輻射模型與建筑性能模擬的耦合計算方法，對光譜選擇性輻射制冷膜應用在建筑表面的物理過程進行刻畫。然而，基于光譜積分方法的耦合模擬計算較為復雜，會大幅度延長輻射膜計算時間。因此，本文對積分加速方法進行了研究，采用分段積分、多元回歸分析和神經網絡算法對光譜選擇性輻射制冷膜的計算進行了簡化，并對計算誤差和加速效果進行了分析。最后，本文以一案例分析說明加速算法的加速效果。

1 研究方法

       1.1 技術路線

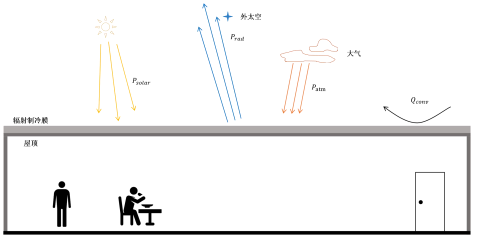
圖1 輻射制冷膜設置在屋頂上時的換熱過程

       本研究首先基于輻射換熱的原理建立了以積分方法計算的輻射制冷膜計算模塊，輻射制冷膜的物理過程如圖 1所示，主要包括輻射和對流兩個過程。對流是指輻射制冷膜表面大氣與膜之間的對流換熱。輻射包括短波和長波兩個部分，其中短波主要包括太陽輻射，由于這部分能量主要集中于可見光和近紅外波段，且輻射制冷膜在此波段的反射率幾乎穩定，因此在計算太陽輻射時可以采用平均發射率。長波輻射包括輻射膜由于具備溫度而自身發射的輻射，由于輻射膜在大氣窗口處具有高發射率，因此發射的熱輻射可以透過大氣直接到外太空中，然而，輻射膜不可避免地也會吸收部分大氣輻射，這部分以圖中P_atm表示。

       本研究中，采用的輻射膜計算模型如式（1）~式（6）^[11]所示：

       

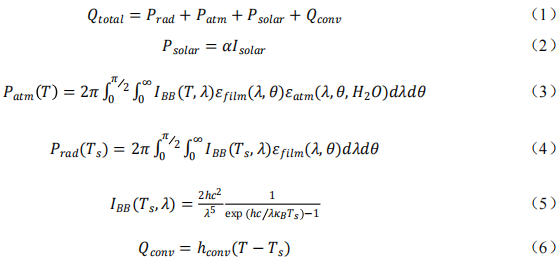
       式中P_rad ——物體表面的輻射強度，W/m²；

            P_atm —— 物體表面吸收的大氣輻射強度，W/m²；

           P_solar ——物體表面吸收的太陽輻射，W/m²；

           Q_conv —— 物體表面與附近空氣的對流換熱，W/m²；

           h_conv —— 對流換熱系數，W/(m²·K)；

           T_s —— 物體表面溫度，K；

           T —— 環境溫度，K；

           I_BB —— 黑體輻射強度，W/(m·Sr)；

           h —— 普朗克常數，6.626×10^-34J·s；

           λ —— 波長，m；

          c —— 真空中的光速，3.0×10⁸m/s；

          κ_B —— 玻爾茲曼常數，1.38×10^-23J/K；

          ε_film —— 輻射膜某波長下的發射率；

          ε_atm —— 大氣某波長下的發射率；

          θ —— 朝向；

          H₂O —— 可降水量，mm；

          α —— 物體表面對太陽輻射的平均吸收率

       本研究中采用的輻射膜發射率曲線如圖 2（a）所示，在3~5和8~13波段具備較高的發射率，在中間波段降低了發射率。大氣發射率曲線由MODTRAN計算得到^{[20, 21]}，主要受大氣中可降水量的影響，從圖 2（b）和（c）中可以發現，隨著可降水量的上升，大氣的吸收能力有所增強，透過性降低。在本研究中，采用線性差值對不同可降水量下的大氣發射率進行計算。

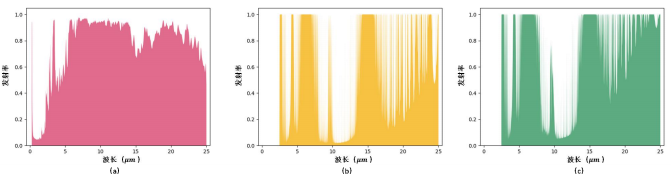
圖2（a）輻射膜發射率曲線（b）大氣發射率曲線（H₂O=3mm）（c）大氣發射率曲線（H₂O=10mm）

       基于上述輻射膜計算方法，通過所要計算的建筑表面溫度、環境溫度，相對濕度和太陽輻射，就可以計算得到輻射過程中交換的熱流，將此熱流輸入建筑性能模擬中，就可以對下一時刻的建筑熱過程進行計算。本研究采用乒乓迭代的方法，實現了這一過程，乒乓迭代方法的耦合原理如圖 3所示。

圖3 通過乒乓迭代法實現輻射膜計算與建筑性能模擬的耦合方法示意圖

       建立輻射膜計算模型后，對不同環境溫度、相對濕度和表面溫度范圍下的多種工況進行計算，得到多工況下的輻射換熱量數據作為加速計算的參考值。本研究采用的工況范圍如表 1所示，共21×9×29=5481種工況，利用輻射膜計算模型運用光譜積分的方法預先計算得到長波輻射換熱量，作為加速算法分析的參考工況。

表1 不同工況的參數取值范圍

       為了提升計算速度，本研究主要采用了三種方法來減少計算量，分別是分段積分法、多元回歸分析和神經網絡算法。分段積分法最為直觀，在長波輻射換熱量較小的波段進行粗糙的積分，在長波輻射換熱量較大的波段進行精細的積分，以最大化計算資源的分配。多元回歸分析通過建立輻射換熱量與環境溫度、相對濕度和表面溫度之間的回歸關系得到長波輻射換熱量，但有可能無法回歸處擬合度較好的結果。神經網絡采用多個神經元作為節點來擬合長波輻射換熱量，不具備明顯的物理規律，對于輸入敏感，且擬合度較高，但是可能存在訓練時間長的問題。

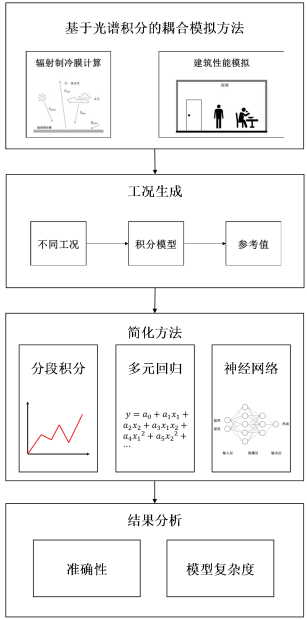
圖4 本研究的技術路線

       如圖 4所示，本研究包含建模、工況生成、簡化方法研究和結果分析。由于簡化后必然造成計算精度的降低，但是為工程應用需要，本研究以計算輻射膜長波輻射換熱量絕對誤差不超過10W/m²為評價指標。在此精度下，本研究試圖給出綜合評價較好的簡化計算方法。

       1.2 分段積分

       由于光譜選擇性輻射制冷膜的光學性質并不是在全波段上都發生劇烈變化的，因此，最直接的簡化方法就是通過分段積分，減少積分次數，以平均發射率和逐波長發射率結合的方式減少單個工況下積分過程的運算量，同時保證輻射制冷膜的制冷效應依然存在。

       本研究以圖 2（a）中的光譜選擇性輻射制冷膜曲線為本研究選取的研究對象，進行簡化，具體方法是，從第一個點開始向后遍歷，在波長位于0~8之間時，當發射率與當前點偏差小于0.1時，則忽略此波動，當發射率與當前點超過0.1時，則記錄當前點和發射率，兩點之間的平均發射率取前者的發射率；在波長位于8~13之間時，當發射率與當前點偏差小于0.003時，則忽略此波動，當發射率與當前點超過0.003時，則記錄當前點和發射率，兩點之間的平均發射率取前者的發射率。在波長位于13~25之間時，當發射率與當前點偏差小于0.05時，則忽略此波動，當發射率與當前點超過0.05時，則記錄當前點和發射率，兩點之間的平均發射率取前者的發射率。按照上述方法進行簡化，得到如圖 5所示的簡化曲線，可以發現簡化的曲線基本能夠反映真實值的特征，在3~5和8~13處均具備較高的發射率，在其他長波段發射率相對較低。

       按照如圖 5所示的簡化發射率曲線，原真實輻射膜發射率曲線共有樣本點14766個，簡化后，樣本點共322個，減少了97.8%。

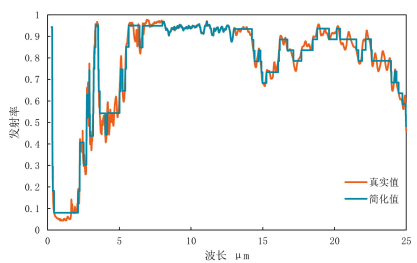
圖5 分段積分簡化后的輻射膜發射率曲線

       1.3 多元回歸

       多元回歸由于模型形式簡單、擬合計算快速等優勢在簡化輻射膜計算的過程中運用廣泛。本研究采用如式（7）~式（8）的回歸方程來擬合輻射熱交換量，由于式（7）在形式上為線性關系，在某些情況下，可近似將輻射視作線性換熱過程，在建筑性能分析中的線性矩陣求解中可以有效提升計算效率[22]。

       

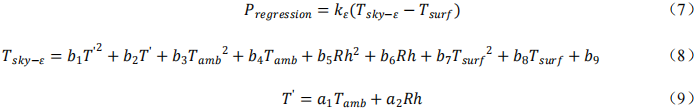
       式中P_regression —— 回歸總輻射交換量，W/m²；

                     T_sky-ε —— 等效天空背景輻射溫度，℃；

                         T’ —— 環境溫度修正，℃；

                          R_h —— 相對濕度，%；

                            k_ε —— 輻射換熱系數，W/(m²·K)。

       式（7）~式（8）中的a_i和b_i均為系數，需根據輻射膜不同的物理性質待定求解。

       1.4 神經網絡

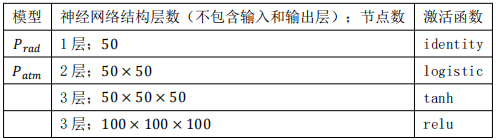
       對于非線性問題的回歸分析，神經網絡算法（ANN）最早由WcCulloch和Pitts等人提出，是一種利用激活函數、矩陣乘法和偏置系數來實現非線性擬合的數據分析方法^[23]。本研究采用如圖 5所示的多層神經網絡結果，主要輸入參數為溫度和相對濕度，輸出參數為輻射交換熱流。本研究分別對P_rad和P_atm分別構建了一組多層神經網絡回歸模型（MLP）。其中，P_rad的輸入參數為T_surf，P_atm的輸入參數為和，選擇的神經網絡結構為1-3層，采用的模型最優解求解方法為Adam方法^[24]，模型評價指標為平均絕對誤差，為防止過擬合，采用5折檢驗的交叉檢驗方法，具體的超參數遍歷范圍如表 2所示。

圖6 本研究中采用的神經網絡算法的基本結構示意圖
表2 神經網絡的超參數選取

2 算法分析結果

       2.1 分段積分

       按照上述方法對輻射膜光譜特性進行簡化后，簡化值與真實值的結果對比如圖 7所示，簡化計算后的結果基本在參考線上，說明簡化值基本與真實值一致。以平均絕對誤差為指標，P_rad的誤差為0.55W/m²，P_atm的誤差為3.62W/m²，P_total的誤差為4.12W/m²，最大誤差為9.64W/m²。總輻射換熱量分布在-733 ~341W/m²之間，此誤差基本可以接受。

圖7 分段積分方法簡化后的P_rad(a)、P_atm(b)和P_total(c)真值與擬合值

       2.2 多元回歸

       經過模型系數待定求解后，模型系數取值如表 3所示。

表 3 針對本研究中選擇的輻射制冷膜對式（8）和式（9）的系數的擬合結果

       如圖 6所示，以多元線性回歸模型經過擬合后的結果如圖，擬合值基本圍繞在參考線y=x附近，說明擬合效果基本良好，輻射換熱量在-733 ~341W/m²之間。定量來看，平均誤差為9.47 W/m²，最大值為39.4 W/m²，此時物體表面溫度與環境溫差均超過40，這在實際過程中幾乎不會發生，因此可被接受。然而，由于上述模型在擬合整體輻射換熱量時使用到了物體表面溫度這一參數，這意味著在進行建筑性能模擬計算時，表面溫度節點仍然需要參與到耦合迭代過程中。

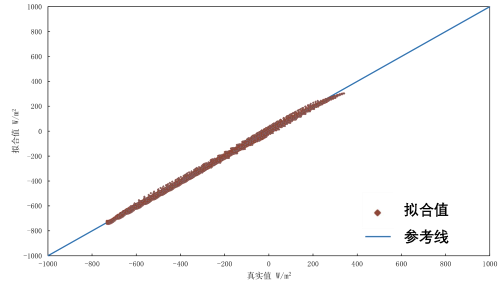
圖8 多元線性回歸擬合值與真實值對比

       2.3 神經網絡

       經過參數自動尋優后，得到兩個模型的最有神經網絡結構分別為：P_rad的輸入參數為T_surf，最優層數為3層，神經元節點個數為，采用的激活函數為修正線性函數relu；P_atm的輸入參數為T和RH，最優層數為3層，神經元節點個數100×100×100，采用的激活函數為修正線性函數relu。

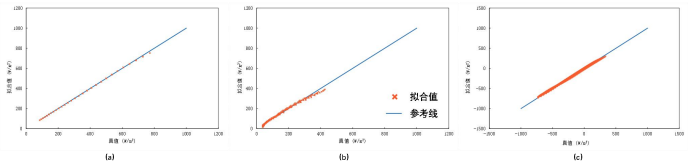
圖9 ANN方法擬合后的P_rad(a)、P_atm(b)和P_total(c)真值與擬合值

       從圖 7可以看出，通過ANN模型訓練后，擬合值與真實值基本圍繞在參考線y=x附近，說明擬合效果較好，以平均絕對誤差為指標，P_rad的誤差為2.87W/m²，P_atm的誤差為8.13W/m²，P_total的誤差為8.95W/m²，最大誤差為41.7W/m²。總輻射換熱量分布在-733 ~341W/m²之間，此誤差基本可以接受。

3 案例分析

       由上述三個方案可以得知，盡管分段積分法并不能以一個簡單模型實現計算結果，但是，通過合理劃分對輻射換熱量起到主要影響的波段，大幅降低積分計算空間，反而能起到較好的簡化結果。因此，本節通過一個案例建筑，說明經過分段積分簡化后，計算時間的減少。

       本演技采用某一商場為研究對象，其建筑模型如圖 10所示，因為建筑面積大，空間復雜，因此在建筑性能模擬時計算復雜，本研究中設置了46個表面為輻射膜表面。

圖10 商場建筑模型圖

       當不采用輻射膜直接計算時，需要的CPU計算時間為2160.0s，當直接采用輻射膜計算時，計算時間為2275.9s，多耗費用時116s，當采用分段積分法簡化后，計算時間為2189.3s，近多耗費用時29.3s。

4 結論

       輻射制冷膜通過選擇性吸收和發射輻射的方式實現物體表面降溫，是實現高效制冷的重要技術手段。傳統建筑性能模擬中對長波輻射的假設無法準確刻畫這類輻射制冷膜的制冷效應，因此需要采用耦合模擬方法，對長波輻射換熱進行單獨計算。然而，這種耦合方法會顯著增加計算代價，本研究采用了三種方法對積分過程進行了簡化，其中分段積分法準確度高，平均絕對誤差為4.12W/m²，但是對于不同表面而言，不同波段的敏感度可能不一樣，在本研究中，對不同敏感波段按照波動值超過0.003,0.05和0.1分別保留真實物性，起到了比較好的結果；多元回歸法模型形式簡單，但是擬合結果相對較差，平均絕對誤差為9.47 W/m²，最大誤差為39.4W/m²；神經網絡算法盡管對超參數進行了遍歷，平均絕對誤差為8.95W/m²，最大誤差為41.7 W/m²，且對不同物性的輻射制冷膜，均需要獨立進行超參數調優，從實用性和方便性的角度來說不如前兩種方法。因此，本研究以一個大型商場為例，分析了計算成本，當采用分段積分法后，相比于無輻射制冷膜的計算時間增加了29.3s，與未簡化的算法相比，節省用時86.6s。

致    謝

       本研究受清華-瑞凌合作研究項目“光譜選擇性輻射制冷膜在建筑圍護結構上應用的適宜性研究”的支持。

參考文獻

       [1] IEA, The Future of Cooling in China: IEA, 2019.
       [2] SALISBURY J W, D'ARIA D M. Emissivity of terrestrial materials in the 3–5 μm atmospheric window [J]. Remote Sensing of Environment, 1994, 47(3): 345-61.
       [3] SALISBURY J, D'ARIA D. Emissivity of terrestrial materials in the 8-14 m atmospheric window [J]. SPIE MILESTONE SERIES MS, 1997, 134(481-504.
       [4] 張靖周. 高等傳熱學 [M]. 科學出版社, 2009.
       [5] YIN X, YANG R, TAN G, et al. Terrestrial radiative cooling: Using the cold universe as a renewable and sustainable energy source [J]. Science, 2020, 370(6518): 786-91.
       [6] CURTIS O F. Leaf Temperatures and the Cooling of Leaves By Radiation [J]. Plant Physiology, 1936, 11(2): 343-64.
       [7] SHI N N, TSAI C-C, CAMINO F, et al. Keeping cool: Enhanced optical reflection and radiative heat dissipation in Saharan silver ants [J]. Science, 2015, 349(6245): 298-301.
       [8] RAMAN A P, ANOMA M A, ZHU L, et al. Passive radiative cooling below ambient air temperature under direct sunlight [J]. Nature, 2014, 515(7528): 540-4.
       [9] GENTLE A R, SMITH G B. Radiative heat pumping from the earth using surface phonon resonant nanoparticles [J]. Nano letters, 2010, 10(2): 373-9.
       [10] ZHAI Y, MA Y, DAVID S N, et al. Scalable-manufactured randomized glass-polymer hybrid metamaterial for daytime radiative cooling [J]. Science, 2017, 355(6329): 1062-6.
       [11] ZHAO D, AILI A, ZHAI Y, et al. Subambient Cooling of Water: Toward Real-World Applications of Daytime Radiative Cooling [J]. Joule, 2019, 3(1): 111-23.
       [12] MANDAL J, FU Y, OVERVIG A C, et al. Hierarchically porous polymer coatings for highly efficient passive daytime radiative cooling [J]. Science, 2018, 362(6412): 315-9.
       [13] ZHAO D, AILI A, ZHAI Y, et al. Radiative sky cooling: Fundamental principles, materials, and applications [J]. Applied Physics Reviews, 2019, 6(2): 
       [14] CHEN J, LU L. Comprehensive evaluation of thermal and energy performance of radiative roof cooling in buildings [J]. Journal of Building Engineering, 2021, 33(101631.
       [15] ZHAO D, AILI A, YIN X, et al. Roof-integrated radiative air-cooling system to achieve cooler attic for building energy saving [J]. Energy and Buildings, 2019, 203(109453.
       [16] CRAWLEY D B, LAWRIE L K, WINKELMANN F C, et al. EnergyPlus: creating a new-generation building energy simulation program [J]. Energy and Buildings, 2001, 33(4): 319-31.
       [17] WANG W, FERNANDEZ N, KATIPAMULA S, et al. Performance assessment of a photonic radiative cooling system for office buildings [J]. Renewable Energy, 2018, 118(265-77.
       [18] ZINGRE K T, WAN M P, YANG X. A new RTTV (roof thermal transfer value) calculation method for cool roofs [J]. Energy, 2015, 81(222-32.
       [19] FANG H, ZHAO D, YUAN J, et al. Performance evaluation of a metamaterial-based new cool roof using improved Roof Thermal Transfer Value model [J]. Applied Energy, 2019, 248(589-99.
       [20] BERK A, CONFORTI P, KENNETT R, et al. MODTRAN® 6: A major upgrade of the MODTRAN® radiative transfer code; proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), F, 2014 [C]. IEEE.
       [21] BERK A, BERNSTEIN L S, ROBERTSON D C, MODTRAN: A moderate resolution model for LOWTRAN: SPECTRAL SCIENCES INC BURLINGTON MA, 1987.
       [22] YAN D, XIA J, TANG W, et al. DeST—An integrated building simulation toolkit Part I: Fundamentals; proceedings of the Building Simulation, F, 2008 [C]. Springer.
       [23] KLEENE S C, Representation of events in nerve nets and finite automata: RAND PROJECT AIR FORCE SANTA MONICA CA, 1951.
       [24] KINGMA D P, BA J. Adam: A method for stochastic optimization [J]. arXiv preprint arXiv, 2014, 

       備注：本文收錄于《建筑環境與能源》2021年4月刊 總第42期（第二十屆全國暖通空調模擬學術年會論文集）。版權歸論文作者所有，任何形式轉載請聯系作者。