天津大學  程思涵  田喆  吳霞

       【摘  要】服務業消耗能源比例日漸提高，服務部門的大部分能源用于辦公建筑取暖、照明、計算和餐飲。辦公用電又是辦公建筑能耗的重要組成部分，因此，建立高精度的電負荷曲線模型至關重要。本文利用馬爾科夫鏈蒙特卡洛方法，通過轉移概率矩陣建立人員模型，得到有效用電人數；結合統計調研數據，利用不同電器不同時刻不同功率的使用概率，建立了電器模型。結合人員模型和電器模型，通過自下而上的建模思想得到日負荷曲線分布。所建模型具有系統性和通用性，仿真與實測對比分析驗證了本文模型的可行性與準確性。

       【關鍵詞】自下而上，馬爾科夫鏈，蒙特卡洛，電負荷

0 引言

       近年來，我國經濟水平飛速發展，建筑能耗水平也隨之不斷增長，辦公建筑能耗作為我國建筑能耗的重要組成部分，其中電能占了很大比例。隨著社會經濟發展，辦公用電仍有很大增長空間^[1]。同時，辦公建筑日負荷曲線的獲取有利于推進智能電網、需求響應等技術的發展^[2,3]。因此辦公建筑日負荷曲線建模很有必要。

       目前，有兩種常用的電負荷曲線建模方法：一種是統計的方法，另一種是自下而上的方法。在統計方法中，研究對象是基于一組測量的負荷曲線，用其來描述輸入數據的特征，然后根據提取的特征制定負荷模型[4]；而在自下而上的方法中，終端電器是研究對象，重點是各個終端電器的使用模式制定，并以此得到總用電量^[5,6]。

       關于統計建模方法，文獻[7]采用時變多元回歸模型來進行電負荷建模，作者考慮到用戶行為和公用事業生產效率變化，可以得到小時級的負荷曲線結果。王等人^[8]提出了一種分解方法，通過分解測量數據以提取不同時間尺度(如季節和工作日)模式，進而模擬電力需求趨勢。斯蒂芬等人^[9]假設電力負荷服從非平穩多元高斯分布，進而提出了一個分析國內能源客戶消費習慣的框架。關于自下而上建模方法，Paatero和Lund^[10]根據季節和社會因素，將單個電器的啟動建模為隨機過程，利用兩個主要數據集作為輸入構建了一個兩級模型：第一級定義了為每個家庭設置的家用設備以及總體負荷波動趨勢，第二級借助最終使用的啟動概率來模擬每個家庭中的每個電器。Stoke在^[11]中提出了一個可以生成三種類型聚合負荷曲線模型：第一層根據相關負荷和電器數據歸一化建模，得到普通家庭的30分鐘需求曲線，第二層考慮到家庭收入、生活方式等得到指定住宅的30分鐘需求曲線；第三層通過對啟動概率建模來得到具有精細分辨率的選定家庭的1分鐘需求曲線。Capasso等人^[12]基于在意大利進行的使用時間調查，建模了單個電器的開始和持續時間，以及附加到每個電器的電力負載，通過匯總單個電器的消耗來建立住宅區的負荷曲線。Walker和Pokoski^[13]對這一模型進行了改進，其人行為建模的基礎是使用兩種概率函數，分別稱為可用性函數和傾向性函數，然后將其推廣到Capasso等人的模型中。C. Sandels等人^[14]利用馬爾科夫鏈模擬辦公人員在室狀態，從而建立自下而上模型生成北歐具有代表性的辦公樓用電負荷曲線。

       從上述研究可以看出來，統計建模方法可以利用宏觀經濟、能源價格和收入以及其他區域或國家指標，更易于開發和使用，還不需要詳細數據。但是這種方法并沒有提供太多細節和靈活性，從而導致精度不夠，而且需要大樣本。另外，統計建模方法通常難以解釋和調查用戶行為的影響。顯然，自下而上的方法雖然需要大量能夠反映家電消費行為的數據，但預測精度很高。對于自下而上方法來說，其模型主要存在三方面的不同：對成員行為描述的詳細程度、對影響電器負荷分布的電器數據描述詳細程度以及所使用的隨機方法。在現有的文獻研究中，很少有人既考慮到成員行為的隨機性又考慮到電器使用數據的隨機性。因此，本文綜合考慮到成員行為以及電器使用功率和概率情況，建立了基于馬爾科夫鏈蒙特卡洛方法的自下而上電負荷曲線模型。

       本文利用馬爾科夫鏈蒙特卡洛方法，通過轉移概率矩陣得到室內有效用電人數，建立了人員模型；結合統計調研數據，利用不同電器不同時刻不同功率的使用概率，建立了電器模型。通過自下而上的建模思想結合人員模型和電器模型，得到日負荷曲線分布。所建模型具有系統性和通用性，適用于需求側管理以及智能電網研究。

1 辦公建筑日負荷建模體系

       對于辦公建筑的電負荷來說，可以分為基礎負荷和與人員行為有關的負荷，基礎負荷即對應電器功率保持固定值或者呈一定周期變化。對于與人員有關的負荷來說，建筑內人的行為會影響到對應電器的使用情況，建筑內人行為具有較大的隨機性，但是因為辦公建筑內部人員具有相對固定的作息時間，所以人員行為又具有一定的規律性，因此結合人員行為構建辦公建筑日負荷曲線模型具有重要意義。

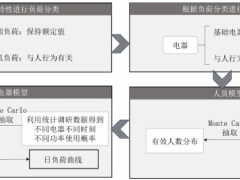
       本文的辦公建筑日負荷曲線建模體系如圖1所示，首先根據負荷特性將負荷分為與人員行為有關的負荷和基礎負荷，進而找到對應的電器。對于基礎電器來說，某確定時刻的功率即為額定功率。對于與人有關的電器來說，首先通過轉移概率矩陣建立人員模型，得到有效使用電器的人數；然后，根據統計調研數據，得到電器在不同時刻不同功率的使用概率，據此建立電器模型。根據人員模型和電器模型獲得單個電器的日負荷分布曲線，再疊加所有電器得到房間的日負荷曲線分布情況。

圖1 基于馬爾科夫鏈蒙特卡洛方法的自下而上辦公建筑日負荷曲線建模體系

2 辦公負荷人員模型

       電器的使用情況并不是完全隨機的，很大程度受到室內人員的影響。本文基于英國TUS（Time-Use Survey）數據庫^[15]，利用馬爾科夫鏈蒙特卡洛方法來生成有效用電人數。英國TUS 數據庫對大量辦公建筑進行調研，以15min為統計精度， 記錄1天24 h活動日程，可以由此統計出1天內各時刻參與者的活動位置，得到建筑內的人員數量及其從事各種活動的概率。

       2.1 MCMC方法

       MCMC方法是一種特殊的蒙特卡洛方法，其將隨機過程中的馬爾科夫鏈應用于蒙特卡洛模擬中，抽樣分布隨模擬的進行而改變，從而實現動態模擬。

       馬爾科夫過程基于如下的思想：若隨機過程在時刻t_i 的狀態已知，且在時刻t>t_i 的狀態僅與時刻t_i的狀態有關，而與t_i前的狀態無關，這個特性稱為馬爾科夫性或無后效性^[16]。馬爾科夫鏈模型基于狀態轉移矩陣( 即從某一狀態轉移到另一狀態的概率) 建立，其中一階馬爾科夫鏈表示一個隨機序列的條件概率只與前一時刻的系統狀態有關， 而與之前的系統狀態無關。其狀態轉移概率矩陣 P 如下所示：

                           （1）

       2.2 有效用電人數

       建筑內電器的使用與有效用電人數密切相關，有效用電人數指的是某一時刻正在使用電器的人數。基于TUS數據庫，每15分鐘建立一個狀態轉移矩陣，考慮到某些房間可能人數較多，故房間人數分區間設置，分別為總人數的10%，20%...100%。利用MCMC方法仿真各時刻的有效人數nt如下公式：

       n_t=f(n,P_i,j,t)          （2）

       其中的n為總人數，P_i,j為轉移概率，公式如下：

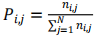                  （3）

       它表示由狀態i轉移到狀態j的次數除以狀態i的總轉移次數，比如P_1,2表示上一時刻的有效人數占比為0.1轉移到下一時刻有效人數占比為0.2的概率。各時刻室內有效人數仿真流程如下圖2：

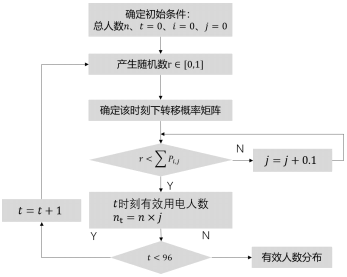
圖2 有效人數生成的算法流程

       （1）確定總人數n，初始時刻設置為0，初始狀態設置為有效人數占比0；

       （2）基于統計數據，利用MCMC方法，將生成的隨機數與不同時刻轉移概率矩陣的累計概率比較，確定不同時刻的有效人數；

       （3）循環96次，得到有效人數在一天內的分布情況。

3 電器模型

       由前述可知，辦公建筑內的電器可以分為基礎電器和與人有關的電器。基礎電器的瞬時功率即為當前時刻的額定功率，計算公式如下：

       P_b,T=P_e,T                  （3）

       其中P_e,T為T時刻該電器的額定功率。

       接下來主要講述如何確定與人有關電器的瞬時功率值，計算流程如下圖3所示：

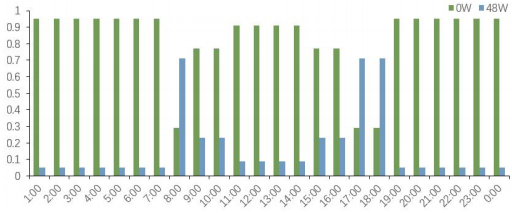
圖3 與人有關電器的瞬時功率值計算流程

       （1）根據統計數據，得到不同電器不同時間不同功率的使用概率，這里將設備的功率值按照實際情況分為不同的檔數，假設為k檔。

       （2）利用隨機數與累計概率比較，確定單臺某電器在T時刻的功率如下公式：

                       （4）

       其中L^m_k代表電器m在第k檔的功率值，β為隨機數，p_T,i表示T時刻不同檔位功率的概率。

       （3）結合人員模型確定的有效用電人數，再引入共用系數α，得到T時刻某設備的功率如下公式：

        P_m,T=Σ^ant_i=1P_m,s,i                  （5）

       其中，n_t為有效人數，i為進行蒙特卡洛抽取的次數，α為共用系數，反應電器共用情況，公式如下：

                                      （6）

       其中A為同時使用人數。

       （4）將這一過程循環M次就可以得到與人有關的設備總功率的瞬時值，公式如下：

       P_p,T=Σ^M_m=1P_m,T          （7）

       其中M表示設備種類。

4、辦公建筑日負荷曲線仿真

       辦公建筑的負荷特征由建筑內人員行為和開啟的電器共同決定，結合人員模型和電器模型可以得到辦公建筑日負荷曲線。

       4.1 仿真結構

       辦公建筑日負荷曲線仿真結構如圖4所示。結合人員模型和電器模型可以得到單個電器功率分布，進而得到所有與人有關的電器功率分布，再加上基礎電器，將各時刻所有電器負荷曲線疊加即可獲得日負荷曲線，日負荷瞬時值如下公式：

       P_T=P_b,T+P_p,T                 （8）

       其中P_b,T為基礎電器瞬時功率，P_b,T為與人有關電器瞬時功率。

圖4 辦公建筑日負荷曲線仿真結構圖

       4.2 模型校驗

       4.2.1 案例介紹與模型數據來源

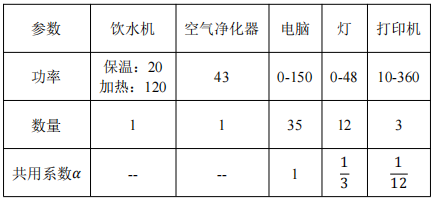
       為了驗證該辦公建筑日負荷曲線模型的有效性，選取某行政辦公樓的某一房間進行校驗。該辦公室共有35人，電器擁有情況為飲水機1臺，空氣凈化器1臺，電腦35臺，燈12個，打印機3臺。作息時間為9:00-17:00，周末休息。具體電器情況見下表1：

表1 辦公室內電器情況

       通過調研得知，打印機的工作功率為360W，不工作時的待機功率為10W；12盞燈采用“一開全開，一關全關”的狀態，打開時功率為48W，關閉時為0，所以對于打印機和燈來說均為兩檔功率。對于電腦來說，通過實際調研發現其功率分布在0-150W之間，故每10W設置為一檔位。對辦公室內的電器進行為期一周的實際使用情況監測，每天每15分鐘記錄一次使用情況，從而得到不同電器不同時間段的使用情況。由于該辦公樓為行政辦公樓，加班情況較少但是也不排除，故結合國家統計局的相關數據資料，將非工作時間的電器使用概率均假設為0.05。由此，辦公室內電器不同時刻不同功率的使用概率如下圖5-7。

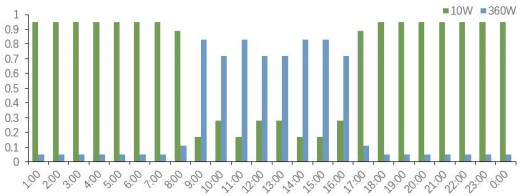
圖5 打印機不同時刻不同功率使用概率

圖6 燈不同時刻不同功率使用概率

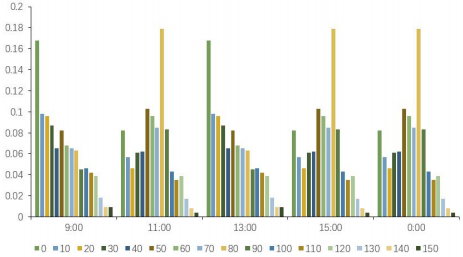
圖7  電腦不同時刻不同功率使用概率

       4.2.2 仿真結果與分析

       根據前述辦公室的信息，利用MCMC方法，得到的有效人數分布情況如下圖8，從有效人數分布來看，上下午各有一個峰值，午休時間會有一個谷值，這是由于辦公建筑的固定工作時間造成的，工作時間之外還考慮到一定的加班情況，故也有較少人數分布。

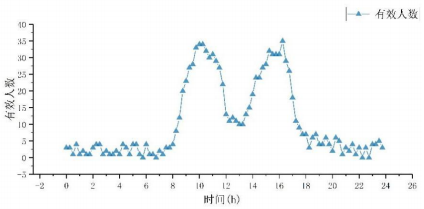
圖8 有效人數分布情況

       平均日負荷曲線通常用來作為選擇配電系統元件容量的標準。故將一周5天工作日的模型數據與實測數據平均值作對比，以驗證所建模型的有效性。圖9是該辦公室一周5個工作日的功率均值對比情況。由圖9看出，模型結果與實測數據具有較好的相似性。

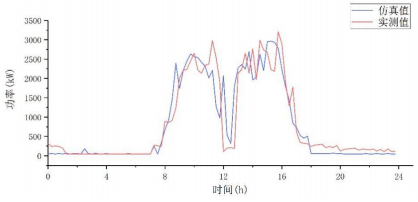
圖9 該辦公室日負荷均值仿真值與實測值對比

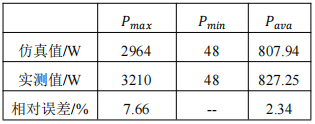
       將5天內模型數據與實測數據的最大值、最小值及平均值作對比，以驗證所建模型的有效性。如下表2所示，因為有一定的基礎負荷晝夜保持運行，故最小值一致，對于最大值和平均值來說，最大相對誤差為7.66%，在可接受范圍內，仿真值與實測值具有較高一致性，故模型較為準確。

表2 電負荷最大值，最小值以及平均值的仿真值和實測值對比

       該辦公室一周5天工作日的概率密度曲線如圖10所示。可以看出，實測值與仿真值的概率密度曲線具有良好的一致性。

圖10 該辦公室功率概率密度曲線仿真值與實測值對比

5 結論

       本文基于統計調研數據，利用馬爾科夫鏈蒙特卡洛方法建立了自下而上的辦公建筑日負荷曲線模型。利用馬爾科夫鏈蒙特卡洛方法建立人員模型得到有效使用電器人數；利用統計調研數據，確定不同電器不同時間不同功率的使用概率，據此建立電器模型。結合人員模型和電器模型得到日負荷分布情況。仿真與實測結果具有良好一致性，證實模型有效。該模型可以應用于需求側管理、智能電網以及配電網動態研究，具有重要工程價值。

參考文獻

       [1] 王葵, 李建超, 潘貞存,等. 居民用戶諧波調查及仿真分析[J]. 電力系統保護與控制, 2008(22):88-92.
       [2] 黃海新, 鄧麗, 文峰,等. 基于實時電價的用戶用電響應行為研究[J]. 電力建設, 2016, 37(2):63-68.
       [3] 朱海明. 電動汽車充電模式對主動配電網的影響[J]. 大科技, 2015, 36(028):97-102.
       [4] Hoverstad, B.A.；Tidemann, A.；Langseth, H. Short-term load forecasting with seasonal decomposition using evolution for parameter tuning[J]. IEEE Trans. Smart Grid 2015(6):1904–1913.
       [5] Chuan L ，Ukil A . Modeling and Validation of Electrical Load Profiling in Residential Buildings in Singapore[J]. IEEE Transactions on Power Systems, 2015, 30(5):2800-2809. 
       [6] Swan L G , Ugursal V I . Modeling of end-use energy consumption in the residential sector: A review of modeling techniques[J]. Renewable & Sustainable Energy Reviews, 2009, 13(8):1819-1835.
       [7] Dordonnat V , Koopman S J , Ooms M , et al. An Hourly Periodic State Space Model for Modelling French National Electricity Load[J]. Tinbergen Institute Discussion Papers, 2008.
       [8] [ Chi-hsiang Wang, Grozev G , Seo] S . Decomposition and statistical analysis for regional electricity demand forecasting[J]. Energy, 2012.
       [9] Stephen B , Mutanen A J , Galloway S , et al. Enhanced Load Profiling for Residential Network Customers[J]. IEEE Transactions on Power Delivery, 2014, 29(1):88-96.
       [10] Paatero J V , Lund P D . A model for generating household electricity load profiles[J]. International Journal of Energy Research, 2010, 30(5):273-290.
       [11] Stokes M . Removing barriers to embedded generation : a fine-grained load model to support low voltage network performance analysis[J]. De Montfort University, 2005.
       [12] Capasso A , Grattieri W . A bottom-up approach to residential load modeling[J]. IEEE Transactions on Power Systems, 1994, 9(2):957-964.
       [13] Walker C F , Pokoski J L . Residential Load Shape Modeling Based on Customer Behavior[J]. IEEE Power Engineering Review, 1985, PER-5(7):34-34.
       [14] Sandels C , Brodén, D, Widén, J, et al. Modeling office building consumer load with a combined physical and behavioral approach: Simulation and validation[J]. APPLIED ENERGY -BARKING THEN OXFORD-, 2016, 162:472-485.
       [15] Milanovic J V , Yamashita K , Martinez Villanueva S , et al. International Industry Practice on Power System Load Modeling[J]. IEEE TRANSACTIONS ON POWER SYSTEMS PWRS, 2013, 28(3):3038-3046.
       [16] Nijhuis M , Gibescu M , Cobben J F G . Bottom-up Markov Chain Monte Carlo approach for scenario based residential load modelling with publicly available data[J]. Energy & Buildings, 2016, 112.

       備注：本文收錄于《建筑環境與能源》2021年4月刊 總第42期（第二十屆全國暖通空調模擬學術年會論文集）。版權歸論文作者所有，任何形式轉載請聯系作者。