浙江正泰能效科技有限公司      丁偉翔   倪岳通   張鶯

摘   要：建筑能耗預測與人工智能模型的相結合是值得研究的課題之一。本文闡述了支持向量回歸SVR模型的搭建方法，針對一棟虛擬的三維辦公建筑，采用能耗模擬的方式獲取空調系統能耗作為訓練集，并通過模型參數的設置及6個特征數的選取等一系列步驟建立了SVR能源預測模型，最后通過測試集對該模型的性能進行了評價。結果表明，經數據樣本訓練后所獲得模型的預測值與真實值之間的方均誤差MSE為0.015，該SVR模型的預測精度達到合格要求，可以用來指導預測未來能耗，為建筑節能領域提供了方法與參考。

關鍵詞：支持向量回歸；數據挖掘；空調系統；能耗預測；數據分析；方均誤差

       0   引言

       回歸預測是數據分析領域的一項重要應用。如圖1所示，是一個簡單的一元回歸預測模型。從歷史統計收集的數據點集合中，希望學習到一個f (x)，將影響目標值y的因素找出來，建立了影響因素x與目標值y之間的函數關系的近似表達式。當f(x)與y偏離不大（通過誤差檢驗），則認為該回歸模型合理。如果模型確定，就可以用該模型對未來/未知因素的變化值進行預測。顯然，回歸模型的建立是一種機器學習的過程，使計算機能夠執行需要人類智能處理的任務^[1]。

圖1   回歸預測模型示意圖

       1   能耗預測與人工智能結合

       隨著建筑全生命周期中的用能占社會總能耗的比率不斷增加^[2]，對建筑能耗進行分析、預測為建筑低能耗的實現提供理論指導和評估依據，是建筑節能降耗的重要措施，對提高建筑能源利用率具有重要意義。作為建筑能耗中占比最大的HVAC能耗，其受到諸多因素的影響：氣象、環境、圍護結構、居住者行為、設備性能、控制策略等，不再是受單一因素影響，而是一種多因素、非線性交互耦合影響的結果^[3]。如式（1）所示，其復雜性使得難以準確預測。

       傳統意義上，建筑空調系統能耗預測方法主要包括兩種：第一種是簡化的能耗指標法，其參考了同建筑業態的往期統計指標，例如夏熱冬冷地區辦公建筑的全年能耗約束值在70~110kW·h/(m²·a)^[4]。第二種是溫度頻率法，其考慮將干球溫度作為影響能耗的主要因素，統計出室外某一溫度范圍的全年總小時數，進而再由相應的計算公式得出能耗值。這兩種方法均是以一種近似的方式評估空調系統的用能水平，而無法精確地得出某特定地區建筑的能耗高低。

       選用合適的模型分析能源情況是值得研究的課題。一個有效且高效的模型一直是工程界尋求的目標。基于人工智能的模型在解決包括大量獨立參數和非線性關系的復雜環境應用問題時具有很大的潛力，可以為建筑能耗預測帶來創新性的技術^[5-7]。與預測相關的使用最廣泛的人工智能方法與高能力人工智能模型是支持向量機（SVM，Support Vector Machine）。SVM模型是從歷史統計數據中提取模型的一組方法，它們通常用于為輸入與輸出之間的復雜關系進行建模或發現數據中的模式。通過對模型進行訓練和測試，挖掘數據中的有效信息，使模型具有高預測精度，是解決分類/回歸問題最好的監督學習算法^[8]。

       顯然，對于建筑空調能耗而言，是一組隨時間連續變化的值，預測能耗涉及到回歸的問題。支持向量回歸SVR（Support Vector Regression）是支持向量在函數回歸領域的應用。如下圖所示：巨大的數據集（圖中的點）構成了一個高維度的向量空間。SVR模型旨在找到一個回歸平面（圖中的實線），讓一個集合內的所有數據到該平面的距離最近（總方差最小），且給定容忍值ζ（圖中的虛線）以防止過擬合（過擬合不具有泛化能力），那么此時得到的超平面就是預測模型。這將回歸轉化為一個最優化的問題。SVR模型通過映射技術解決非線性擬合問題而引入核函數，使得該算法在高維特征空間中有效地工作^[9]。

圖2   SVR模型示意圖

       目標函數為式（2）：

       約束條件為式（3）：

       最終SVR模型的決策式為式（4）：

       式中：_αi*，αi為拉格朗日乘子，K(x_i, x)為核函數。

       本文探究人工智能模型與建筑空調能耗預測、能源工程領域相結合的可行性。通過對歷史能耗數據的挖掘與學習，訓練并測試出相應的SVR模型，用以預測該建筑未來的能耗，為人工智能在建筑節能領域中的應用提供參考。

       2   SVR模型建立過程

       圖3展示了SVR模型的學習過程：將所采集的歷史統計數據分為訓練集和測試集，統稱為數據樣本。兩種樣本均由目標值（逐時能耗值）與特征值（影響能耗值的變量因素）組成，即用以訓練/測試模型的數據樣本應有目標值和特征值的完整描述。在能耗預測模型中，所篩選的特征數應與能耗有較大的相關程度。具體步驟如下^[10]：

     （1）首先，運用訓練集，設置相關參數，完成對數據的學習，生成SVR模型。

     （2）其次，將測試集中的特征值輸入所生成的SVR模型中，輸出通過該模型所得到的預測目標值。

     （3）再次，將預測目標值與測試集目標值（真實值）進行對比，評價該模型的性能。

     （4）最后，若所獲得的模型通過評價達到合格，則可將該模型應用于實際；否則，調整優化模型參數設置，重新訓練模型。

       顯然，擁有充足的樣本數有助于訓練模型精度的提升，充分和準確的能耗數據對模型的評價十分重要。因此，在訓練模型之前，如何收集足夠多的數據樣本是模型開發的首要問題。通常的收集方法是通過安裝于現場實地的傳感器監測采集歷史數據。然而，由于影響能耗值的因素較多，實際測量難以獲取每個變量的逐時時間序列，造成數據顆粒度不足，且測量耗時長，可能測量誤差。本文的主要目的是探究人工智能模型在能耗預測中的可行性，通過合理地設置與校準仿真軟件，采用模擬的方法可以產生與實際很接近的數據^[11]。此處采用DeST能耗模擬軟件，建立了一個虛擬的三維建筑模型，設置相關的邊界條件，輸出建筑內空調系統的逐時能耗及各個影響因素的瞬時值作為歷史數據樣本，即認為此時能耗模擬數據就是真實數據。

       3   建筑模型假設

       現建立一個簡易模型，為一棟位于杭州地區的三層辦公樓，圍護結構熱工性能均滿足國家標準GB 50189–2015《公共建筑節能設計標準》^[12]。夏季室內制冷的空調系統采用風機盤管+新風的半集中形式，冷源為冷水機組，機組恒溫出水（7℃），一次泵定流量運行。室內設計溫度為26℃，空調開啟時間為每日8:00~17:00。以8月份整個月份的逐時能耗（此處的能耗為整個空調系統，包括了冷水機組+水泵+風機盤管+新風機組）作為研究對象——其中，1日至25日的能耗數據作為訓練集（10×25=250個樣本）進行模型的學習，26日至31日的能耗數據作為測試集（10×6=60個樣本）以判斷預測模型的精確度。

圖4   辦公樓標準層平面圖及三維建筑模型

       DeST能耗模擬軟件對整個建筑及系統有完整的描述，如表1所示。

表1   杭州某辦公樓熱環境外擾/內擾條件

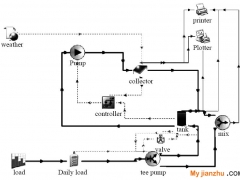
       仿真的過程如圖5所示。

圖5   建筑能耗模擬過程

       特征數作為變量是影響能耗的重要因素。特征數的選取極大地影響模型的性能，對于模型的開發而言是重要的。一般而言，所選取的特征數與目標值相關程度越高，預測就越準確。然而，并非特征數的數量越多越好，盲目追求提高預測精度會引發“維數災難”（隨著特征數的增加，計算量呈指數倍增長的一種現象）。合理地篩選最契合目標值的特征數，可以對模型進行簡化，起到減少訓練時間的作用[13]。此處給定了六個影響能耗的特征數，認為他們與能耗大小的相關程度較高，包括：1、室外溫度2、太陽輻射量3、新風負荷4、室內人員數5、冷水機組回水溫度6、冷水機組COP，即這六個特征數構成了預測模型的支持向量（SV，Support Vector）。因此，建立SVR模型過程的拓撲圖如圖6所示。

圖6   支持向量拓撲圖

       表2為通過能耗模擬所得出的用作訓練與測試的數據樣本。數據集的每個樣本都是以單位小時為時間序列的數值。基于訓練集來表示目標對特征的依賴關系，產生高預測精度的高性能模型，而通過測試集來評價模型的預測性能。

表2   訓練集樣本與測試集樣本

       進一步地設置相應的參數建立SVR模型：支持向量機的類型選取ε—SVR；核函數的類型選取RBF徑向基函數，其易于使用且很好地解決了非線性問題；最好的模型參數應該具有很好的預測未知數據的能力而不會引起過擬合問題，由“循環遍歷算法”計算所得的懲罰因子（表征對離群點的重視程度）C=10000，參數gamma=0.025。

       4   預測結果分析評價

       將測試集中的目標值（真實值，圖中的藍線）與訓練出的SVR模型所得出的預測值（圖中的紅線）繪制于同一曲線圖中進行對比，數據樣本是8月26日8時至8月31日17時的總計60個樣本（NO.251~NO.310）。采用式（5）“均方誤差（MSE，Mean Square Error）（圖中的綠線）”作為評價指標[14]，判斷經訓練后的模型的準確性。

       式中：ytrue為真實值，yprediction為預測值。

       從圖7中可以看出，基于歷史數據擬合出來的SVR模型的預測性能非常好，測試集中的目標值與預測值十分接近。兩者總體的均方誤差MSE=0.015。此時，可認為所建立的SVR模型合理，精確度達標。分析擬合程度如此高的原因：一方面，能耗值（目標值）與影響因素（特征值）之間的規律性極強，能耗對所選擇的6個特征數展示出很好的依賴性。另一方面，SVR模型在數據挖掘方面的性能良好，泛化能力強，適用于能耗數據的回歸擬合。

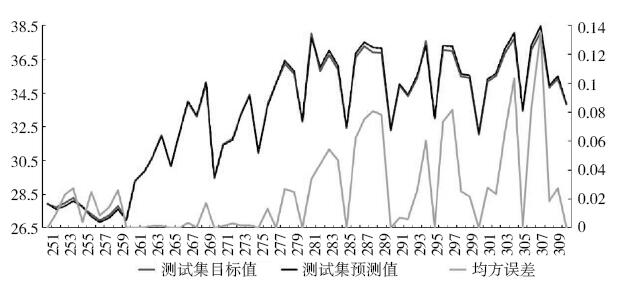
圖7   真實值與SVR模型預測值的對比結果

       既然依據上述步驟，通過歷史數據的訓練集訓練出了SVR模型，又通過測試集驗證了模型的精確性及可靠性。那么，此模型便可用以分析未來的某一特定條件下的能耗值。任意給定上述特征數的具體數值，便可以計算出在此種邊界條件的描述下建筑空調的能耗。例如，現任意給定一組特征數——室外溫度35℃，太陽輻射量200W/m²，新風負荷100kW，室內人員數100人，冷水機組回水溫度10℃，冷水機組COP值5，則通過該模型預測的空調系統能耗為35.0876 kW·h。

       5   結論

       本文闡述了人工智能模型與建筑能耗預測兩者相結合的可行性。針對模擬搭建的一棟位于杭州的辦公建筑，通過模型的介紹、能耗的仿真、參數的設置、特征數的選取以及預測性能的評價等步驟，建立了關于該棟建筑空調系統能耗預測的SVR模型，得出的結論如下：基于歷史數據集訓練得出的SVR模型，挖掘了數據中的潛在信息。經測試后，其預測值與真實值的總體方均誤差僅為0.015，模型的精確性合格，能夠用于預測未知未來的能耗。可見，支持向量回歸模型SVR可以用來解決非線性、多影響因素的回歸問題，即使少量的數據樣本，只要模型選擇和參數設置合理，可以提供非常準確的預測，為建筑能耗的預測與分析提供了一種方法與參考。

參考文獻

       [1] 陳凱, 朱鈺. 機器學習及其相關算法綜述[J]. 統計與信息論壇, 2007, 22(5):105–112.

       [2] 谷立靜, 郁聰. 我國建筑能耗數據現狀和能耗統計問題分析[J]. 中國能源, 2011, 33(2):38–41.

       [3] 丁勇, 劉學, 黃渝蘭,等. 空調系統節能量測量與驗證方法的應用分析[J]. 暖通空調, 2018, 48(07)：47–54.

       [4] 中國建筑科學研究院. GBT 51161–2016, 民用建筑能耗標準[S]. 北京：中國建筑工業出版社，2016:9.

       [5] Mocanu E, Nguyen P, Gibescu M , et al. Deep learning for estimating building energy consumption[J]. Sustainable Energy, Grids and Networks, 2016, 6(6):91–99.

       [6] Ahmad A S , Hassan M Y , Abdullah M P , et al. A review on applications of ANN and SVM for building electrical energy consumption forecasting [J]. Renewable and Sustainable Energy Reviews, 2014, 33(5):102–109.

       [7] Constantine E.Kontokosta，ChristopherTull. A data-driven predictive model of city-scale energy use in buildings [J]. Applied Energy, 2017, 197(1):303–317.

       [8] 丁世飛, 齊丙娟, 譚紅艷. 支持向量機理論與算法研究綜述[J]. 電子科技大學學報, 2011, 40(1):2–10.

       [9] 陳博, 鄭凱東, 王家華. 多核支撐向量回歸方法研究[J]. 智能計算機與應用，2019, 9(01):191–194.

       [10] 弗雷德里克.馬爾古斯. 建筑能耗分析中的數據挖掘與機器學習[M]. 趙海祥等,譯.北京：機械工業出版社, 2018:48–51.

       [11] 燕達, 陳友明, 潘毅群, 等. 我國建筑能耗模擬的研究現狀與發展[J]. 建筑科學, 2018, 34(10):130–138.

       [12] 住房和城鄉建設部標準定額研究所. GB 50189-2015, 公共建筑節能設計標準[S]. 北京：中國建筑工業出版社, 2015:10–11.

       [13] 陳啟買, 陳森平. 支持向量機的一種特征選取算法[J]. 計算機工程與應用, 2009, 45(23):49–51.

       [14] 李云雁, 胡傳榮. 試驗設計與數據處理.第2版[M]. 化學工業出版社，2017:146–147.

備注：本文收錄于《建筑環境與能源》2019年5月刊總第21期。
                 版權歸論文作者所有,任何形式轉載請聯系作者。