天津科技大學機械工程學院      朱傳琪   田瑋   張安朝   史佳鑫

天津市建筑設計院      尹寶泉

摘   要：為研究不同輸入參數對于辦公建筑能耗的影響，并確定辦公建筑能耗的概率密度分布，聯合使用建筑能耗模擬程序EnergyPlus以及統計學R語言，進行辦公建筑能耗的不確定性和敏感性分析。首先通過拉丁超立方法對所研究參數在給定范圍內抽樣，得到模型輸入參數組合，然后利用R語言和EnergyPlus完成數百個模型的自動建模。最后對能耗計算結果進行不確定性分析和敏感性分析。不確定性分析可得到辦公建筑取暖、制冷能耗的分布情況，而敏感性分析能確定影響辦公建筑的取暖和制冷能耗的主要參數。根據敏感性分析和不確定性分析結果可為新建建筑節能設計及既有建筑節能改造提供指導。

關鍵詞：建筑能耗；自動建模；拉丁超立方抽樣；敏感性分析；不確定性分析

基金項目：國家自然科學基金項目（51778416）；教育部哲學社會科學研究重大課題攻關項目（16JZD014）。

       0   引言

       根據《中國建筑能耗研究報告（2017年）》^[1]，2015年我國建筑能源消費總量為8.57億噸標準煤，占全國能源消費總量的20%。其中公共建筑能源消費達3.41億噸標準煤，占全國建筑能源消費總量的39.8%。因此，探究公共建筑能耗特性并提出相應的節能措施，對于降低建筑能耗促進建筑節能發展有重要意義。

       由于影響建筑熱性能的參數具有很強的不確定性^[2]，包括人行為、室內得熱、建筑圍護結構性能參數等。為了達到量化這些參數不確定性的目的，不確定性分析已經廣泛應用于建筑能耗分析的各個領域，包括能耗模型校驗^{[3, 4]}、生命周期分析^{[5, 6]}、建筑優化改造^[7]等。另一方面，敏感性分析可確定影響建筑能耗的主要因素，其中全局敏感性分析法可用于確定建筑能耗輸入和輸出參數之間的復雜關系，并可考慮變量間的相互作用，所以這種全局性敏感性分析方法引起研究者廣泛的興趣。Patrick等利用敏感性分析方法研究在設計階段建筑能耗模型中各個參數對建筑能耗的影響^[8]。Joseph C·Lam等利用敏感性分析方法研究建筑能耗結果提出建筑改造措施^[9]。但目前大多數研究采用的是確定性和局部敏感性分析方法^{[10, 11]}，不能全面準確的考慮建筑能耗不確定性，并無法準確提供影響建筑能耗因素的重要性排序。

       辦公建筑作為公共建筑中典型的建筑類型，具有建筑數量多、使用能耗高的特點。故本文主要選取天津地區辦公建筑作為研究對象，采用基于蒙特卡洛抽樣的全局敏感性分析和不確定性分析方法，對辦公建筑能耗特點進行分析，研究影響辦公建筑能耗的主要因素以及辦公建筑能耗的概率分布。

       1   研究方法

       1.1   研究步驟

       本研究主要分為五步（如圖1所示）：第一步首先進行能耗模型的構建，通過確定辦公建筑研究參數的分布，并對每個參數在其分布中進行拉丁超立方抽樣，得到辦公建筑輸入參數的組合。然后使用R語言的文字編輯功能，將抽樣得到的參數與EnergyPlus構建的基礎能耗模型結合，完成能耗模型的構建。第二步運行所得的EnergyPlus辦公建筑模型，并通過R語言對建筑能耗模型計算結果進行收集整理。第三步，對于建筑能耗模擬結果進行不確定性分析，得到建筑能耗的均值、偏度、峰度等統計量和概率密度函數等可視化結果。第四步采用樹形高斯過程和多元自適應回歸樣條進行全局敏感性分析。第五步，根據不確定性分析和敏感性分析結果，確定影響建筑辦公建筑能耗的關鍵參數以及能耗分布，并提出優化措施。

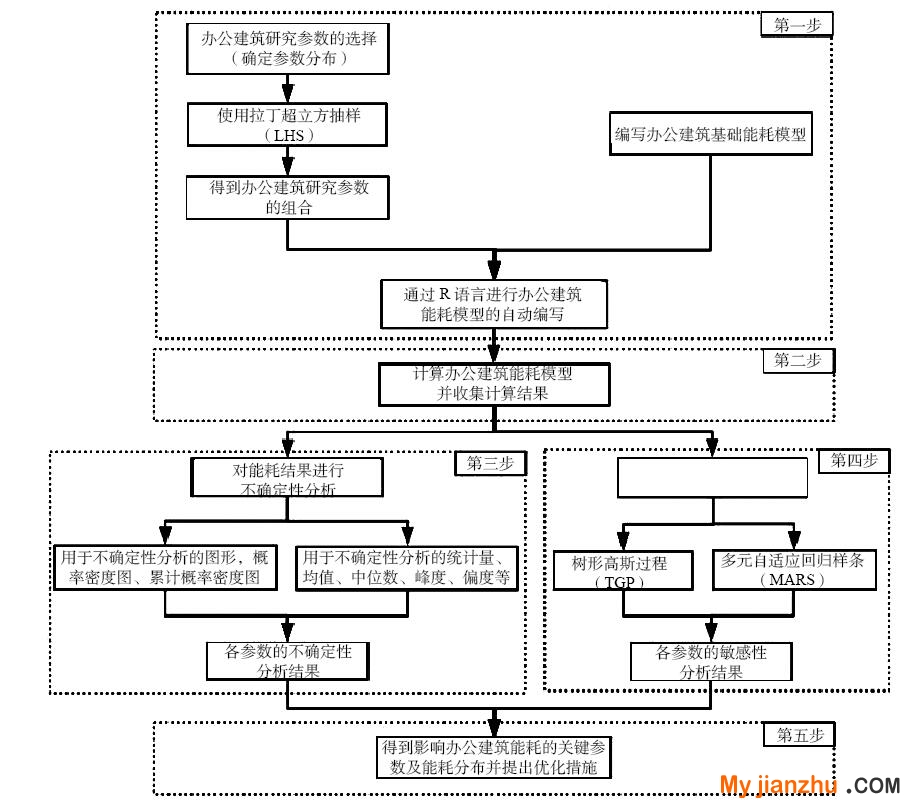
圖 1   建筑能耗的不確定性及敏感性分析研究流程圖

       1.2   能耗模型構建

       本文選擇建立天津地區的辦公建筑模型進行建筑能耗計算及分析。為便于模型的建立，所建立的模型建筑的長寬比均為2，建筑的朝向均為北向。建立的辦公建筑模型的不確定性參數包括建筑的體形系數、建筑各個方向的窗墻比、窗戶的傳熱系數、太陽得熱系數、外墻傳熱系數、建筑層數、照明功率密度、設備功率密度、人均占有建筑面積以及換氣次數等參數，這些參數總結于表1。

表 1   研究選取的不確定性參數變量

       由于本文為設計性問題，故表1中參數均服從均勻分布，各個參數的范圍按照國標GB 50189–2015《公共建筑節能設計標準》^[12]中的規定選取。根GB 50189–2015中的規定，其中窗戶的傳熱系數和太陽得熱系數兩個參數只有相應的上限值，因此根據查閱相應的文獻獲得窗戶傳熱系數以及太陽得熱系數的下限值。對于換氣次數通過查閱相應的文獻選取換氣次數的范圍，具體的參數范圍以及參考文獻見表1。所建立的建筑模型如圖2，需要說明由于建筑的很多參數均為變量，所以圖2只是其中的一種參數組合所形成的建筑模型。天津地區絕大多數辦公建筑的暖通空調系統為風機盤管^{[17, 18]}，因此本文選擇風機盤管作為辦公建筑的暖通空調系統。使用EnergyPlus進行建筑能耗模擬時需要相應地區的天氣數據，本文選擇由EnergyPlus提供的天津地區典型年氣象數據作為進行建筑能耗計算時的天氣數據。

圖 2   辦公建筑模型示意圖

       1.3   不確定性分析方法

       影響建筑能耗的因素有很多，比如人均占有建筑面積、設備使用時間表、空調設定溫度，這些因素都具有很強的不確定性。因此，如何定量化的分析建筑能耗中的這些不確定性因素受到越來越多的關注^[2]。不確定性分析方法可以分為兩大類：正向不確定性傳遞和逆向不確定性計算。如果已知建筑中與熱性能相關的輸入參數，通過建筑能耗模型，得到建筑能耗的概率分布，這屬于正向不確定性傳遞。正向不確定性關注于從輸入參數的不確定性通過模型計算量化輸出的不確定性。逆向不確定性分析，則是根據建筑能耗實測值和能耗模型，計算建筑能耗模型中的未知參數。正向不確定性的結果可以通過統計量指標或圖形進行表示，常用于表示不確定性的統計量指標包括均值，中位數，標準差等，常用于表示不確定性的圖形可采用柱狀圖、箱線圖、概率密度函數圖以及累計概率密度函數圖表示。本文選擇正向不確定性分析，通過正向不確定性分析得到天津地區辦公建筑能耗分布，并通過相應的方式來表示不確定性分析結果。

       1.4   敏感性分析方法

       敏感性分析方法已經廣泛的應用于建筑能耗分析中^[19]。敏感性分析是研究模型中輸入變量在其變化范圍內變動對輸出變量影響大小的分析方法^[20]。樹形高斯過程是結合了高斯過程和決策樹，是一種貝葉斯非平穩和非線性回歸模型^[21]。根據元模型法的步驟，首先通過樹形高斯過程根據輸入變量和輸出變量建立代理模型，然后使用這個代理模型并結合基于方差的敏感性分析，得到敏感性分析結果。樹形高斯過程的敏感性分析結果有主效應和全效應兩個指標，主效應和全效應指標的數值越大說明其對結果的影響越大。其中主效應表示各個輸入變量單獨變化對輸出變量的影響，全效應則是考慮了各個變量之間的交互作用之后輸入變量對于輸出變量的影響。主效應通過計算各輸入變量單獨作用引起模型輸出變量的方差與輸出總方差的比值得到的，全效應通過計算各個輸入變量及其交互作用引起的模型輸出變量的方差與輸出總方差的比值得到的。主效應與全效應的差就是輸入變量交互作用的影響。具體計算公式為^[11]：

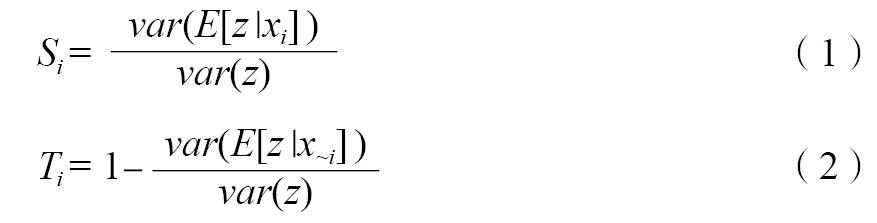
       式（1）（2）中：S_i 為主效應；T_i 為全效應；xi為輸入變量；x~i 為不包括；x_i 的其余輸入變量；z為模型輸出。

       2   結果與討論

       2.1   不確定性分析

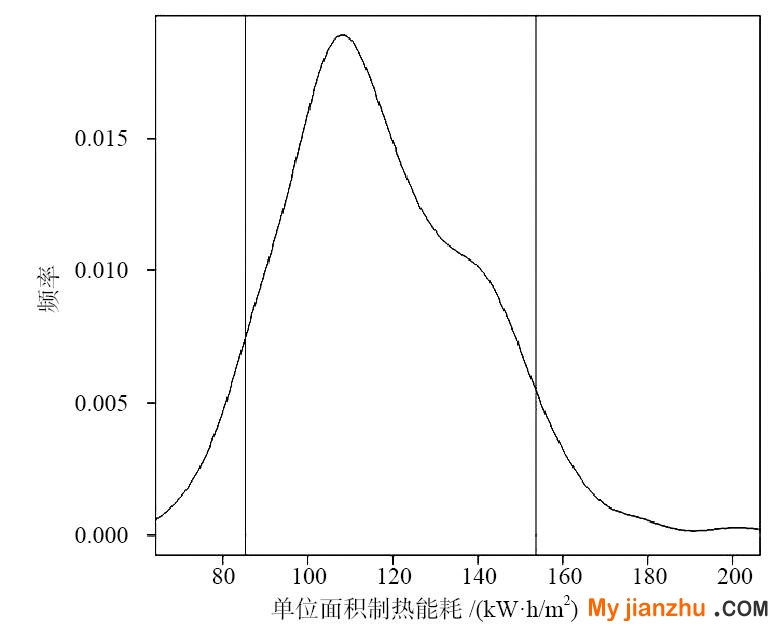
       對于辦公建筑取暖能耗不確定性分析結果，從圖3中可以得到辦公建筑的單位面積取暖能耗的均值為117.21kW·h/m²，中位數為114.18kW·h/m²。單位面積取暖能耗的分布呈現為中間高兩邊低，即大部分辦公建筑的單位面積取暖能耗相差不大，而單位面積取暖能耗過高以及過低的建筑較少，單位面積取暖能耗90%的置信區間為85.35kW·h/m²~153.62kW·h/m²。通過單位面積取暖能耗概率密度圖可以得出，概率密度函數的偏度系數為0.53，峰度系數為3.38。

（a）單位面積取暖能耗累積概率密度圖	（b）單位面積取暖能耗概率密度圖

      圖3   取暖能耗不確定性分析

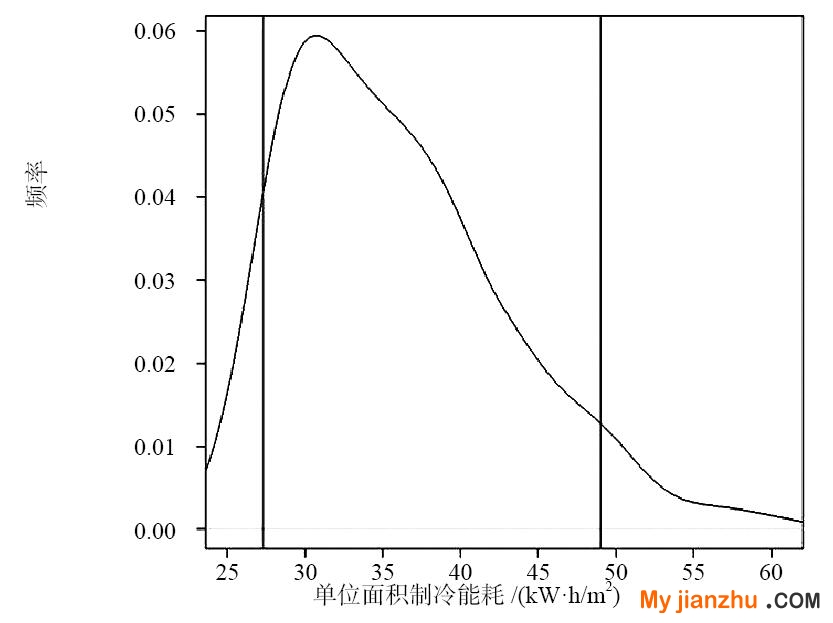
        對于辦公建筑制冷能耗不確定性分析結果，從圖4中可以得到辦公建筑單位面積制冷能耗的均值為35.98kW·h/m²，中位數為34.81kW·h/m²。單位面積制冷能耗的分布呈現左高右低的趨勢，辦公建筑單位面積制冷能耗的標準差為7.03，說明辦公建筑單位面積制冷能耗較為集中。單位面積制冷能耗的分布比較集中在能耗相對低的范圍，即大部分辦公建筑的單位面積制冷能耗相差不大，而單位面積制冷能耗過高的建筑較少，單位面積制冷能耗90%的置信區間為27.30kW·h/m²~49.01kW·h/m²。通過單位面積取暖能耗概率密度圖可以得出，概率密度函數的偏度系數為0.87，峰度系數為7.04。

（a）單位面積制冷能耗累計概率密度圖	（b）單位面積制冷能耗概率密度圖

圖4   制冷能耗不確定性分析

       2.2   敏感性分析

       圖5表示取暖能耗的全局敏感性分析結果，最重要的三個參數是：人均占有建筑面積、窗戶的傳熱系數以及太陽得熱系數。而層數和設備功率密度等對于取暖能耗的影響較小。對于敏感性排序較后的參數則說明其對于取暖能耗的影響較小，在進行辦公建筑能耗計算及分析時可適當忽略這些影響較小的參數，主要考慮影響較大的參數來簡化能耗計算過程，降低能耗模型的復雜性。

（a）主效應隨輸入變量的變化	（b）全效應的變化區間

圖 5   取暖能耗樹形高斯過程敏感性分析

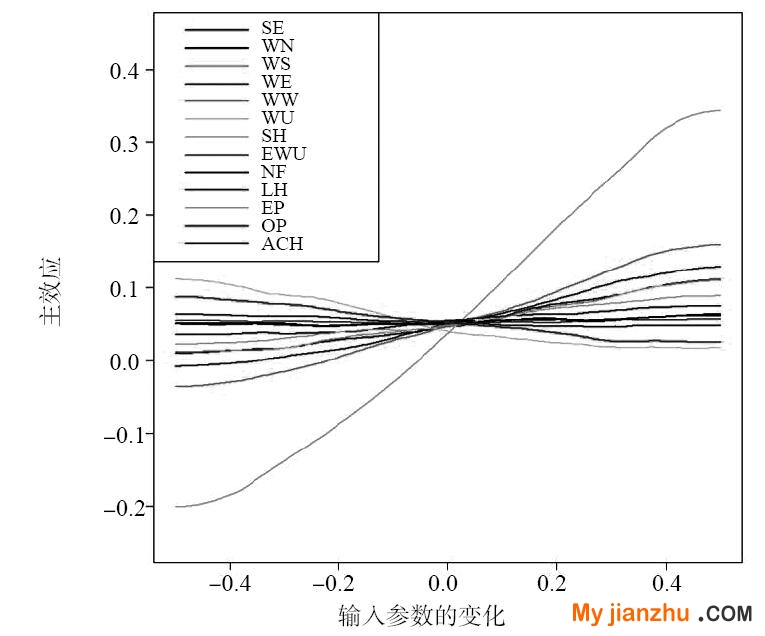
       圖6表示制冷能耗的全局敏感性分析結果。對于辦公建筑制冷能耗影響較大的參數為太陽得熱系數以及建筑各個方向的窗墻比。通過敏感性分析結果可以發現，辦公建筑窗戶的傳熱系數以及建筑中的人均占有建筑面積與辦公建筑制冷能耗的關系為負相關，即窗戶的傳熱系數越大以及人均占有建筑面積越大則建筑的制冷能耗越小。但是，窗戶的傳熱系數以及人均占有建筑面積的變化只能在一定范圍內使得制冷能耗有所降低，當窗戶的傳熱系數增加到2W/m²·K以及人均占有建筑面積分別增加9m²/人后，其對于制冷能耗的影響基本不變化。對于人均占有建筑面積而言，一方面隨著人均占有建筑面積的持續增加由人散發出的熱量就較減少這便會降低建筑的制冷能耗；另一方面風機盤管系統新風量的能耗相比由人產生的能耗要高，所以也會導致這種情況。對于窗戶的傳熱系數而言，如果傳熱系數過小，則會導致建筑內部的熱量不能很好的散失，使得建筑內部的熱量都需要空調系統排出，導致增加了建筑的制冷能耗，但如果窗戶傳熱系數的太大，則會導致通過空調系統產生的冷量通過窗戶散失出去，增加制冷能耗。

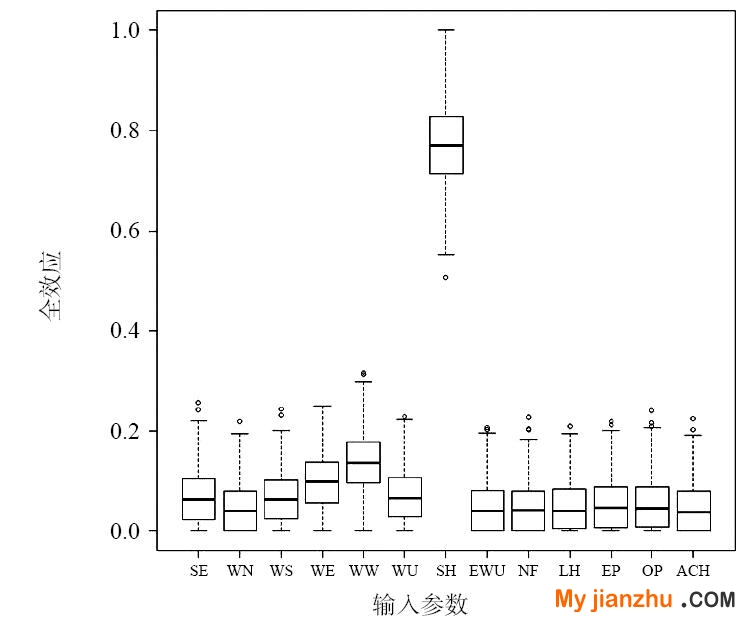（a）主效應隨輸入變量的變化	（b）全效應的變化區間

圖 6    制冷能耗樹形高斯過程敏感性分析

       3   結論

       通過對辦公建筑能耗計算結果的不確定性分析，可以得到通過輸入參數不確定性所導致的能耗結果的不確定性，得到辦公建筑單位面積取暖能耗、制冷能耗的分布。然后，基于不確定性分析結果，在給定輸入參數的條件下來預測建筑能耗。

       通過樹形高斯過程敏感性分析結果，對于辦公建筑取暖能耗而言，對其影響較大的參數主要為人均占有建筑面積，窗戶的傳熱系數以及太陽得熱系數。對于辦公建筑制冷能耗而言，對其影響較大的參數為太陽得熱系數、建筑在各個方向的窗墻比以及窗戶的傳熱系數。對辦公建筑能耗進行的敏感性分析，其結果可以幫助新建建筑設計以及既有建筑改造，也可以根據敏感性分析結果把對能耗影響較小的參數刪除或者簡化考慮，以降低模型的復雜程度以及縮短模型的計算時間。

參考文獻

       [1] 侯恩哲. 《中國建筑能耗研究報告(2017)》概述[J]. 建筑節能, 2017, (12):131.

       [2] Tian W, Heo Y, Wilde P D, et al. A review of uncertainty analysis in building energy assessment[J]. Renewable & Sustainable Energy Reviews, 2018, 93:285–301.

       [3] Heo Y, Choudhary R, Augenbroe G A. Calibration of building energy models for retrofit analysis under uncertainty[J]. Energy & Buildings, 2012, 47(4):550–560.

       [4] Kristensen M H, Choudhary R, Petersen S. Bayesian calibration of building energy models: Comparison of predictive accuracy using metered utility data of different temporal resolution[J]. Energy Procedia, 2017, 122:277–282.

       [5] Hoxha E, Habert G, Lasvaux S, et al. Influence of construction material uncertainties on residential building LCA reliability[J]. Journal of Cleaner Production, 2017, 144:33–47.

       [6] Häfliger I-F, John V, Passer A, et al. Buildings environmental impacts’ sensitivity related to LCA modelling choices of construction materials[J]. Journal of Cleaner Production, 2017, 156:805–816.

       [7] Rezvan A T, Gharneh N S, Gharehpetian G B. Robust optimization of distributed generation investment in buildings[J]. Energy, 2012, 48(1):455–463.

       [8] Shiel P, Tarantino S, Fischer M. Parametric analysis of design stage building energy performance simulation models[J]. Energy and Buildings, 2018, 172:78–93.

       [9] Lam J C, Wan K K W, Yang L. Sensitivity analysis and energy conservation measures implications[J]. Energy Conversion & Management, 2008, 49(11):3170–3177.

       [10] 王永龍, 潘毅群. 典型辦公建筑能耗模型中輸入參數單因子敏感性的分析研究[J]. 建筑節能, 2014, (02):9–14.

       [11] 何成, 朱麗, 田瑋. 城市建筑布局的能耗敏感性分析 [J]. 哈爾濱工業大學學報, 2018, 50:174–180.

       [12] 中國建筑科學研究院. 公共建筑節能設計標準:GB50189-2015 [M]. 中國建筑工業出版社, 2015.

       [13] 馮雅. 《公共建筑節能設計標準》中外窗及幕墻熱工參數的確定 [J]. 暖通空調, 2005, 35:44–47.

       [14] 王蘇穎, 狄洪發. 窗戶太陽得熱對嚴寒地區采暖能耗影響的研究  [C]; 全國暖通空調制冷2002年學術年會, F, 2002.

       [15] 張旭, 周翔, 王軍. 民用建筑室內設計新風量研究[J]. 暖通空調, 2012, 42(7):27–32.

       [16] 孫越霞, 侯靜, 張慶男, 等. 天津市居住建筑新風量的測量與分析 [J]. 暖通空調, 2016, 46:10–13.

       [17] 李文朝. 天津地區辦公建筑節能研究 [D]; 天津大學, 2014.

       [18] 陳高峰, 張歡, 由世俊, 等. 天津市辦公建筑能耗調研及分析 [J]. 暖通空調, 2012,42:125–128.

       [19] Tian W. A review of sensitivity analysis methods in building energy analysis[J]. Renewable & Sustainable Energy Reviews, 2013, 20(4):411–419.

       [20] 蔡毅, 邢巖, 胡丹. 敏感性分析綜述[J]. 北京師范大學學報(自然科學版), 2008, 44(1):9–16.

       [21] Gramacy R B, Taddy M. Categorical Inputs, Sensitivity Analysis, Optimization and Importance Tempering with tgp Version 2, an R Package for Treed Gaussian Process Models[J]. Journal of Statistical Software, 2010, 33(i06).

備注：本文收錄于《建筑環境與能源》2019年5月刊總第21期。
                 版權歸論文作者所有,任何形式轉載請聯系作者。