天津科技大學機械工程學院      田瑋   張安朝   朱傳琪   史佳鑫

天津市建筑設計院      尹寶泉

摘   要：機器學習可建立計算速度快的建筑能耗統計模型，方便于進行不確定性、敏感性、最優化等研究，機器學習模型精度受很多因素影響，如輸入變量數目、抽樣方法、樣本數量等。本研究重點探究樣本數量對機器學習模型預測精度的影響。機器學習方法選取多元自適應回歸樣條法，以位于天津的辦公建筑為例進行研究。結果表明，當建筑能耗分析中樣本數量較少時，由于信息缺失導致建筑能耗輸入變量間交互作用無法體現。隨著樣本數量的增加，建筑能耗機器學習模型可以表示出輸入變量間的復雜交互作用，并且建筑能耗機器學習模型中所需的項數也增加。研究還發現，樣本數量的增加，不僅可提高建筑能耗機器學習模型的預測精度，而且可提高模型預測精度的穩定性。

關鍵詞：機器學習；建筑能耗；樣本數量；模型精度

基金項目：國家自然科學基金項目（51778416）；教育部哲學社會科學研究重大課題攻關項目（16JZD014）。

       0   引言 

       隨著我國建筑能耗的持續增加，為了建立低碳綠色的建筑環境，需要深入了解建筑能耗的特性^[1]。時間序列、空間分析、物理模型、統計模型等不同研究方法^[2]，已經用于解析建筑能耗特點。機器學習做為一種可快速得出能耗計算結果的方法，逐漸在建筑能耗分析中得到廣泛應用^{[3, 4]}。常用的機器學習模型包括神經網絡(neural network)、支持向量機(support vector machine)、隨機森林(random forest)、多元自適應回歸樣條(multivariate adaptive regression splines，簡稱MARS)、集成學習(ensemble learning)、深度學習(deep learning)等^{[5, 6]}。田瑋等^[3]評估了6種不同的機器學習方法，在建筑能耗模型中的適用性。Wei等^[4]比較了不同機器學習算法在預測倫敦建筑能耗時的精度。Ngo等^[7]比較了不同機器學習方法在預測建筑制冷負荷時的誤差。

       這些研究對于了解機器學習模型在建筑能耗分析中特點，有非常好的指導作用。但對于樣本數量對于機器模型的學習精度沒有明確的說明。基于建筑物理模型的機器學習建模，需要一定數量的模型運算得到輸入輸出數據矩陣。樣本數量增多意味著更多的運行時間和成本，所以需要明確樣本數量與機器學習模型精度的關系，確定合適的樣本數量，以得到準確可靠的機器學習模型。

       1   建筑能耗模型

       圖1為研究中所用的三維建筑能耗模型，這是一個位于天津的L型四層辦公建筑。建筑圍護結構的熱工特性，符合我國2015年發布的公共建筑節能標準^[8]。建筑的內部得熱，包括人員、設備和照明的得熱，與2015年節能標準中附錄中的推薦值相同^[8]。采用風機盤管系統提供通風、取暖和制冷，建筑有天然氣鍋爐和風冷式制冷機組提供暖通系統所需的熱水和冷水。建筑能耗模擬采用EnergyPlus V9.0程序^[9]，得到供暖和制冷所需的能耗。

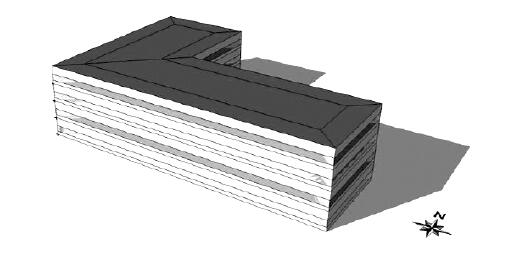
圖1   四層辦公建筑模型

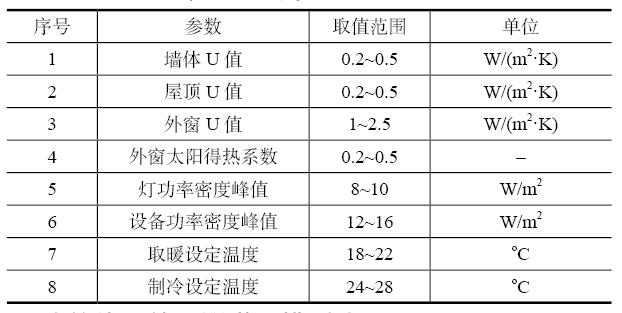
       本文研究重點是建立可靠準確的機器學習模型，所以輸入參數需要有相應的變化范圍，如表1所示。分為3類參數，包括圍護結構的熱工特性、內部得熱和暖通系統參數。圍護結構熱性能參數包括墻體、屋頂和外窗的總傳熱系數。內部得熱包括照明和設備的功率密度。暖通系統參數包括取暖和制冷的設定溫度。由于本文所建立的機器學習模型是為了在這些參數變化范圍內得到盡量可靠的模型，所以這些參數假定為均勻分布。采用拉丁超立方法得到這些參數的不同組合，通過建筑能耗計算得到建立機器學習模型所需的數據樣本集。拉丁超立方法的特點是良好的分層特性[10]，所以可在參數變化的范圍內盡量的分布均勻。為了充分研究不同樣本數量對于機器學習模型精度的影響，研究中選用40、60、100、200、400、800共6個樣本數量。

表1   抽樣參數取值范圍

       2   建筑能耗的機器學習模型建立

       機器學習包括很多不同的算法，如隨機森林、支持向量機、多元自適應回歸樣條、神經網絡等^[11]。研究中選用多元自適應回歸樣條，是因為先前研究表明這種方法有較高的計算精度，并且有計算速度快的優點。多元自適應回歸樣條是擴展后的線性模型，可包括非線性和交互作用。在這種機器學習方法中，使用分段后的新變量而不是原始數據集中的變量，所以可表達輸入變量和輸出變量之間的非線性作用。由于模型結構相對于其它機器學習算法簡單，所以方便于分析不同變量間的交互作用，具有較高的模型可解釋性。

       多元自適應回歸樣條有兩個可調整的參數：模型中變量數目和交互作用階數。模型中的變量數越多，意味著更為復雜的模型，回歸精度會提高，但可能出現過擬，需要采用重抽樣方法避免這種過擬^[6]。交互作用的階數為1時，表示模型中變量間不存在交互作用；階數為2時，表示兩個變量間的交互作用；階數為3時，表示有三個變量間的交互作用。過高的階數可能導致過擬。所以采用重復交叉驗證法，以得到最優的機器學習模型參數，同時避免過擬現象。重復的目的是為減少模型精度估計量的方差，提高模型精度估計的準確程度。模型精度用均方根誤差（root mean sequare error, 簡稱RMSE）表達，RMSE越小表明所得機器學習模型有更高的精度。

       3   結果與討論

       本節首先討論樣本數量對機器學習建模過程的影響，然后分析抽樣數量對機器學習模型最終優化模型參數的影響，最終確定樣本數量對建筑能耗機器學習模型精度及穩定性的影響。

       3.1   樣本數量對機器學習建模過程的影響

       圖2表示不同抽樣數量對于建筑取暖能耗機器學習模型的影響。當抽樣數量為40時，不考慮交互作用模型的精度高于考慮交互作用的模型，表明由于數據過少沒有充分的信息可提取，所以無法得出模型中交互作用，最終所得模型為不考慮交互作用的模型，其預測精度也較低。當抽樣數量為60時，考慮交互作用與否對最終模型沒有影響，其模型預測精度也不高。隨著抽樣數量增加到200時，由于數據量增加更多的信息可以提取，所以交互作用的模型與不考慮交互作用時相比，有更高的精度。當抽樣數量增加到800，與抽樣數量為200時的特點基本一致，但模型精度得到進一步提升。因此，足夠數量的建筑能耗數據是得到準確機器學習模型的前提。

圖2   不同抽樣數量對建筑取暖能耗的機器學習建模優化過程影響

       圖3表示不同抽樣數量對建筑制冷能耗機器學習模型的影響。圖3表示的規律與圖2類似，數據量較小時，由于沒有足夠的信息，不能體現出變量間復雜的交互作用，其模型預測精度也較低。隨著數據樣本的增加，可以反應輸入變量間的本質關系，所以模型的精度有明顯增加，也可以表達變量間的交互作用。 

圖3   不同抽樣數量對建筑制冷能耗的機器學習建模優化過程影響

       3.2   樣本數量對機器學習模型最終優化參數的影響 

       圖4和圖5表示不同抽樣數量對建筑取暖能耗機器學習模型最終參數影響的直方圖，包括模型中項數和相互作用次數。由圖4可以看出，當數據樣本數量增大時，模型中的最終項數也增大，表明數據量的增大帶來信息量增加，模型需要更多的項數才可以表達輸入和輸出之間的函數關系。相互作用的次數也有類似關系如圖5所示，當抽樣數量為40次時，10次重復抽樣所得結果的模型都只需要沒有交互作用的模型。當抽樣數量增加到100次以上時，所有10次重復抽樣所得結果都需要二階交互作用的機器學習模型。

圖4   不同抽樣數量對建筑取暖能耗機器學習模型中最終項數的影響

圖5   不同抽樣數量對建筑取暖能耗機器學習模型中交互作用次數的影響

       對于不同抽樣數量對于建筑制冷模型中最終兩個參數的影響，其影響趨勢與取暖能耗類似。當抽樣數量為40時，制冷能耗機器學習模型有6組抽樣只需要11個項。當抽樣數量為800時，最少的項數也需要15次，有4組甚至需要17次的項數來表達輸入和制冷能耗之間的復雜關系。相互作用階數也隨著抽樣數量的增加而增加。

       3.3   樣本數量對機器學習模型精度的影響 

       圖6表示不同抽樣數量對建筑取暖和制冷能耗的影響，包括10次抽樣和中位數的結果。對于取暖能耗，當抽樣數量從40次增加到60次時，預測精度增加非常明顯，RMSE約減少30%。但當樣本數量增加到100時，增加幅度就變得非常有限。樣本數量400時的精度與樣本數量為800時的精度相差很小。當抽樣數量從40增加到800時，模型精度的中位數值約增加一半。所以足夠數量的樣本是機器學習模型精度取得良好效果的前提。在計算機模擬分析中，通常取10倍變量的樣本數目，可以得到比較好的精度，但取決于項目的需求，如果對于能耗模型精度有更高要求，則更多的樣本數量是必需的。

（a）heating energy                                                                 （b）cooling energy

圖6   不同抽樣數量對建筑能耗機器學習模型精度影響

       由圖6（a）可得出另外一個重要的結論，同樣抽樣數量的樣本，重復抽樣所得的結果非常分散。如抽樣數量為60所得的結果并不必然比抽樣數量為40時，所得結果的誤差小。所得機器模型精度的分散程度隨著樣本數量的增大而減少。所以為了保證模型精度，減少相同樣本數量時所得結果的偏差，增大樣本數量也非常有必要。

       對于制冷能耗的機器學習模型，所得結果與取暖能耗模型類似。模型精度隨著樣本數量的增加有明顯的增加，模型精度隨著抽樣種子的方差隨著樣本數量的增加而減少。所以，樣本數量的增加不僅可以提高建筑制冷機器學習模型的預測精度，而且也提高了預測精度的穩定性。

       4   結語

       本研究分析了樣本數量對于建筑能耗機器學習模型精度的影響，得出了以下結論：

     （1）當建筑能耗分析中樣本數量較少時，由于信息缺失導致建筑能耗的輸入變量間交互作用無法體現。隨著樣本數量的增加，建筑能耗機器學習模型可以表示出輸入變量間的復雜交互作用。

     （2）隨著樣本數量的增加，建筑能耗機器學習模型中所需的項數也增加，相應模型精度也有一定提升。

     （3）建筑能耗分析的樣本數量增加，不僅可以提高建筑能耗機器學習模型的預測精度，而且可以提高模型預測精度的穩定性。

       因此，建筑能耗分析中樣本數量對于機器學習模型精度有明顯的影響，樣本數量選取需依賴于研究項目的具體目的和要求。如能耗分析人員可根據建筑項目特點，確定機器學習模型精度，在此前提下則可根據交叉驗證的結果確定出合適的樣本數量。

參考文獻

       [1] 清華大學建筑節能研究中心. 中國建筑節能年度發展研究報告：2018 [M]. 北京: 中國建筑工業出版社, 2018.

       [2] 金濤, 楊小山, 姚靈燁, 等. 城市局地氣溫對建筑冷負荷的影響 [J]. 建筑科學, 2018,34:32–39.

       [3] 田瑋, 魏來, 李占勇, 等. 基于機器學習的建筑能耗模型適用性研究 [J]. 天津科技大學學報, 2016:54–59.

       [4] Wei L, Tian W, Silva E A, et al. Comparative Study on Machine Learning for Urban Building Energy Analysis[J]. Procedia Engineering, 2015, 121: 285–292.

       [5] Amasyali K, El-Gohary N M. A review of data-driven building energy consumption prediction studies[J]. Renewable and Sustainable Energy Reviews, 2018, 81: 1192–1205.

       [6] Kuhn M, Johnson K. Applied predictive modeling [M]. Springer, 2013.

       [7] Ngo N-T. Early predicting cooling loads for energy-efficient design in office buildings by machine learning[J]. Energy and Buildings, 2019, 182:264–273.

       [8] 中國建筑科學研究院. 公共建筑節能設計標準:GB50189-2015 [M]. 中國建筑工業出版社. 2015.

       [9] DOE, EnergyPlus V9.0.1, October 2018, Department of Energy, USA [R], 2018.

       [10] Tian W, Heo Y, de Wilde P, et al. A review of uncertainty analysis in building energy assessment[J]. Renewable and Sustainable Energy Reviews, 2018, 93:285–301.

       [11] Wei Y, Zhang X, Shi Y, et al. A review of data-driven approaches for prediction and classification of building energy consumption[J]. Renewable and Sustainable Energy Reviews, 2018, 82:1027–1047.

備注：本文收錄于《建筑環境與能源》2019年5月刊總第21期。
                 版權歸論文作者所有,任何形式轉載請聯系作者。