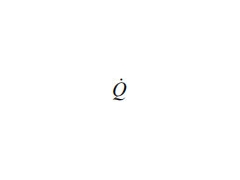崔騰飛¹ 蔡姍姍¹ 刁廣琦² 
1 華中科技大學能源與動力工程學院  2 中鐵第四勘察設計院集團有限公司

    【摘  要】現有的豎直地埋管換熱器分析模型通常忽略地下水流動和鉆孔軸向導熱的影響，且不適用于整個時間尺度的流體溫升預測，普通的線熱源模型產生的熱響應延遲導致流體預測溫升偏大。本文提出了一種同時考慮地下水流動和鉆孔軸向導熱影響的全時間尺度分析模型，適用的時間尺度從幾分鐘到數十年，并在此模型基礎上進一步分析了鉆孔內參數、運行時間和地下水流動對地埋管換熱性能的影響。

    【關鍵詞】地源熱泵；地埋管換熱器；分析解；地下水；全尺度

1 前言

    在很多國家，地源熱泵系統是其淺層地熱能源利用的一種主要方式^{[1, 2]} 。在閉式地源熱泵系統中，流體介質通過豎直或水平地埋管換熱器與土壤進行換熱，可用于環境供熱、空調系統、商業或民用建筑的熱水供應等。豎直地埋管換熱器因占地面積相對較小，受大氣環境和季節變換影響較弱而具有更大的發展潛力。

    傳統的豎直地埋管換熱器傳熱分析方法是將換熱器的傳熱過程分為鉆孔內的穩態傳熱和鉆孔外的非穩態傳熱過程兩部分。鉆孔外的瞬態傳熱模型主要基于Ingersoll^[3]提出的無限長線熱源模型和圓柱熱源模型，因為鉆孔尺寸相對較小（管長/管徑≈150m/0.05m），鉆孔內物質的熱容相對周圍土壤的熱容也很小，所以鉆孔內的傳熱過程可近似為穩態傳熱過程。基于此假設，出現了采用等效直徑處理方法的一維導熱模型、考慮U型支管相互影響的二維模型^[4]以及考慮流體溫度變化相互影響的準三維模型^[5] 。由于冷熱負荷隨時間波動的影響，鉆孔內結構的熱響應時間大概有數小時，因此，鉆孔內穩態傳熱的假設顯然不夠完善。Eskilson^[6]提出鉆孔內穩態導熱的假設要在τ≥5r_b²/a（通常為4～8小時）時才能避免產生較大的預測誤差；Claesson^[7]根據等效直徑假設，得到了從幾分鐘到數十年時間尺度的分析解模型，并且得到線熱源模型與考慮鉆孔內傳熱過程的等效直徑模型相比有一定的時間延遲；Li^[8]提出了非穩態復合介質全尺度模型，考慮了鉆孔內的瞬態傳熱現象，但此模型并不適用于有地下水流動影響的情況。如果在設計階段考慮地下水流動的影響，可節約16%的投資成本^[9] 。目前雖然出現了考慮地下水流動影響的移動無限長線熱源模型和考慮鉆孔軸向導熱的移動有限長線熱源模型，但移動線熱源模型由于不考慮鉆孔內的傳熱過程，所以也不適用于短時間尺度熱響應的分析。

    因此，本文提出了一種同時考慮短時間尺度熱響應、地下水流動和鉆孔軸向導熱影響的分析模型，將提出的模型和傳統線熱源模型和移動線熱源模型進行了對比，并進一步研究了鉆孔內參數、運行時間和地下水流動等對換熱器熱響應的影響。

2 模型基本理論

    有地下水流動時豎直地埋管換熱器的簡圖如圖1所示。假設地下水沿x軸單方向均勻流動，Darcy速度為u_d。

    2.1 不考慮地下水流動的分析解模型

    在工程應用中，鉆孔有較大的長徑比（直徑為0.11～0.2 m，長度為40～200 m），鉆孔可以假設成是一個線熱源，忽略鉆孔軸向導熱。根據無限長線熱源（ILS）模型理論，鉆孔壁面處的溫度G函數見公式（1）[6]。

   

    其中，u為積分變量，E1為指數積分函數。約1.6年之后[10]，忽略軸向導熱影響的無線長線熱源模型會產生很大的誤差，這將導致設計管長增加約15%[11]。考慮鉆孔兩端邊界條件的影響，出現了有限長線熱源理論（FLS），此時鉆孔壁面的積分平均溫度G函數見公式（2）[12]。

   

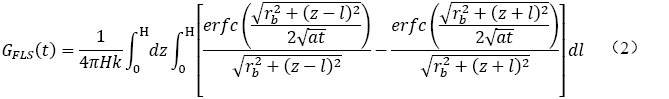
    其中，l、z為積分變量，erfc(x)為余誤差函數。以上模型均是基于鉆孔內為穩態導熱的假設，忽略了回灌材料熱熔和支管布置結構等鉆孔內部參數的影響，不能用于考察鉆孔內的瞬態導熱過程。Li^[13]等在Jaeger的基礎上提出了復合介質線熱源（CMLS）模型，簡圖如圖2所示。將流體進出的兩U型支管假想成無限長線熱源，管外壁面平均溫度可近似認為是A和B兩點溫度的平均值。

    根據無限大介質中線熱源模型，使用A和B兩點的平均溫度得到線熱源溫度G函數如公式（3）至公式（4）所示^{[8, 14]} 。

   

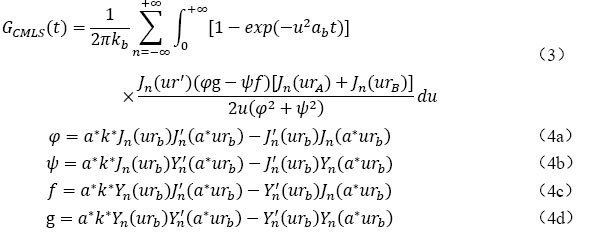
    其中，無量綱熱擴散系數a*=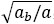，無量綱熱導率k*=k/kb，r´為線熱源位置半徑，r_A、r_B為A和B點的位置半徑，u為積分變量，上式可以使用文獻[15]中給出的簡化數值積分進行計算。

    2.2 考慮地下水流動影響的分析解模型

    上述模型均沒有考慮地下水流動對鉆孔換熱器換熱過程的影響，如果在設計階段不加考慮地下水流動的影響，很可能產生過大設計^[16] 。在均勻初始溫度條件下，Sutton^[17]和Diao^[16]等給出了無限大多孔介質中的移動無限長線熱源（MILS）模型公式。 

   

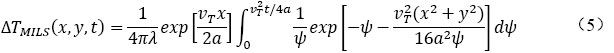
    其中，υ_T=u_d(ρC_p)w/ρC_p為有效熱傳遞速率，引入無量綱量Pe=υ_TH/a,F₀=at/H²，并對整個鉆孔壁面的溫度進行積分，由此可以得到我們關注的鉆孔壁面積分平均無量綱溫度G函數見公式（6） ^[16] 。 

   

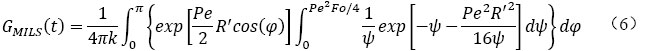
    其中，，ψ為積分變量。Molina-Giraldo等[18]假定地表溫度恒定，土壤為半無限大均勻介質，提出了移動有限長線熱源（MFLS）模型，鉆孔壁面無量綱積分平均溫度G函數表達式見公式（7）至公式（8） ^[18] 。

   

    上面敘述的模型公式可以利用文獻中[19]給出的簡化方法計算。當不考慮地下水流動的影響時（即Pe=0），移動線熱源公式分別退化為無限長線熱源和有限長線源模型公式，見公式（9）。

   

3 考慮地下水流動影響的全時間尺度模型

    傳統的ILS/FLS模型和CMLS模型分別適用于中長時間尺度和短時間尺度無滲流影響的情況，而MILS/MFLS模型適合中長時間尺度有地下水滲流影響的情況。我們發現，ILS/FLS模型和CMLS模型在中時間尺度（tb<Fo<tH）的預測結果相差一個恒定的溫差ΔT，如圖3所示，其公式可表示為公式（10）。

   

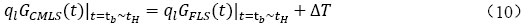
    其中，ΔT為溫度響應延遲量，tb為短時間尺度與沖時間尺度的轉變點，它與鉆孔內參數有關，tH為中時間尺度與長時間尺度的轉變點，它與鉆孔長度有關。根據轉換時間的假設，我們可以得到考慮地下水流動影響的全時間尺度模型CMLS-MFLS，由公式（3）至公式（8）可以得到流體管壁面無量綱平均溫度G函數表達式，見公式（11）。

   

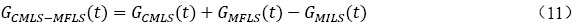
    由此可得到全時間尺度模型CMLS-MFLS的流體管壁面溫度G函數的完整表達式（12）。在一定冷熱負荷作用下的流體平均溫度則可通過公式（13）進行計算。由于公式（12）可通過分段求解的方法進行簡化計算，流體溫升的計算表達式如公式（14）所示。

   

    其中，R_p=[l_n(r_o/r_i)+k_p/(r_ih)]/(2πk_p)為流體支管熱阻，N_u=2hr_i/k_f=0.023Re^4/5Prⁿ，h為對流換熱系數，當流體被加熱時n=0.4，被冷卻時n=0.3。Rb為鉆孔內穩態熱阻，它適用于中長時間尺度的情況。現階段已有眾多方法計算鉆孔穩態熱阻的分析解，部分解析方法如表1所示：

    注：λ₁=r_b/r_o；λ₂=r_b/xU; λ₃=r_p/(2xU);σ=(k_b-k_s)/(k_b+k_s)

    圖4所示為不同鉆孔熱阻模型求解得到的不同管間距下的無量綱鉆孔熱阻值，與COMSOLTM數值解的偏差量如表2所示。從下面對比的結果中可以看出，在不同的管間距下，多級方法預測得到的無量綱鉆孔熱阻最好。因此，將采用多級方法的經驗公式預測鉆孔穩態熱阻Rb。

4 結果與分析

    在模型的求解與分析中，相關參數按表3選取。

    如圖3所示為不同鉆孔材料參數條件下，CMLS模型和常規ILS/FLS模型的熱響應曲線比較。從圖中可以看出，由于線熱源模型不考慮鉆孔內的傳熱過程，所以熱響應過程相比較考慮鉆孔內傳熱的CMLS模型存在一個溫度響應延遲量?T。圖5所示為根據轉換時間（t_b≈7.67小時，t_H≈0.87年）構建出的不考慮地下水流動影響的全時間尺度模型流體溫升隨時間的變化曲線。

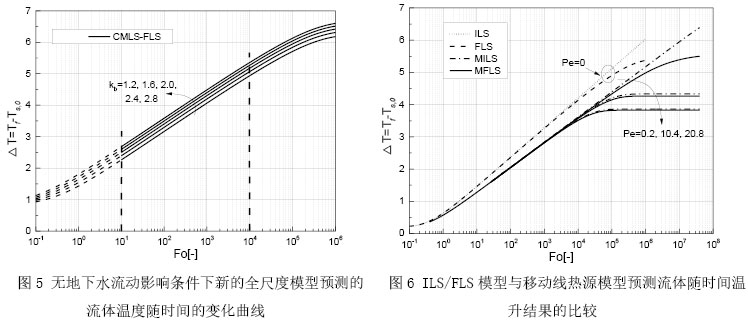
    圖6所示為不同地下水流動速度下，MILS模型和MFLS模型的熱響應曲線。在熱響應初期Fo<104，兩模型的預測結果幾乎一致，說明此時間段內，鉆孔的軸向導熱可以忽略不計；而當Fo>104，兩模型的預測值出現了明顯的差異，該差異隨著Pe數的增大而逐漸減小，說明在較長的時間尺度下，鉆孔軸向的導熱不可忽略，但隨著地下水流動速度的增加，地下水流動對換熱的影響逐漸增強，鉆孔軸向導熱的影響逐漸被削弱。當Pe>10時，地下水流動的影響占優，此時可以忽略軸向導熱的影響；當Pe<0.2時，鉆孔軸向導熱影響占主導地位。隨著Pe數的增大，地埋管的換熱能力逐漸變強，對流換熱達到穩態的時間越來越短。在Fo>10時，移動線熱源模型和常規不考慮地下水流動的線熱源模型預測結果產生了明顯的差異，且隨著Pe數的增大，差異逐漸變大，此時如果繼續使用常規的線熱源模型將會產生較大誤差。

    圖7所示為本文提出的不同地下水流動速度條件下的全尺度模型CMLS-MFLS的流體溫升曲線圖，模型與MFLS模型預測的溫升結果對比如圖8所示。從圖中可以看出，兩類模型的預測值在Fo<10時相對偏差達50%以上，隨著地下水流動速度的增加，兩模型的預測值偏差進一步增大。在地下水流動速度不變的情況下，隨著運行時間的增加，兩模型的預測偏差呈減小趨勢，表明提出的全時間尺度模型可較好的修正移動有限長線熱源模型未考慮鉆孔傳熱過程在短時間尺度內出現較大的預測偏差。

    水流動速度條件下預測得到的流體隨時間的溫升曲線    

5 結論

    在傳統地埋管換熱器傳熱分析模型的基礎上，本文提出了一種全時間尺度CMLS-MFLS模型，模型考慮了地下水流動和鉆孔軸向導熱的影響，能夠可以用于計算短時間尺度單鉆孔熱響應G函數，模型物理概念清晰，與常規分析解求解一樣簡單。以下是得出的主要結論和發現：

    （1）提出的CMLS-MFLS模型具有復合介質線熱源模型考慮鉆孔內傳熱過程的優點，可以有效地避免傳統線熱源模型（ILS/FLS/MILS/MFLS）由于不考慮鉆孔內傳熱過程導致的熱響應延遲，以此適用于短時間尺度地下換熱器的模擬分析。在本文的模擬參數下，新模型可避免的溫度偏差約為0.5℃。

    （2）CMLS-MFLS模型與常規移動線熱源對比結果表明，常規的移動線熱源模型由于忽略鉆孔內導熱和鉆孔軸向導熱，將導致較大的預測誤差。通過分析還可以得到，當地下水流動速度較大時（Pe>10），軸向導熱的影響相比地下水流動對換熱的影響要大很多，此時可以忽略鉆孔軸向導熱的影響。當地下水流動速度較小時（Pe<0.2），地下水流動對換熱的影響可以忽略，此時鉆孔軸向導熱的影響占主導因素。 

參考文獻

     [1] Somogyi V, Sebestyén V, Nagy G. Scientific achievements and regulation of shallow geothermal systems in six European countries – A review[J]. Renewable & Sustainable Energy Reviews. 2017, 68: 934-952.
     [2] Haehnlein S, Bayer P, Blum P. International legal status of the use of shallow geothermal energy[J]. Renewable & Sustainable Energy Reviews. 2010, 14(9): 2611-2625.
     [3] Ingersoll L R, Zobel O J, Ingersoll A C. Heat Conduction with Engineering, Geological, and Other Applications[J]. Journal of Geology. 1954, 63(63): 196.
     [4] Hellström G. Ground heat storage: Thermal analyses of duct storage systems[D]. Sweden: Department of Mathematical Physics University of Lund, 1991.
     [5] Diao N R, Zeng H Y, Fang Z H. Improvement in Modeling of Heat Transfer in Vertical Ground Heat Exchangers[J]. Hvac & R Research. 2004, 10(4): 459-470.
     [6] Eskilson P, Claesson J. Simulation model for thermally interacting heat extraction boreholes [J]. Numerical Heat Transfer Applications. 1988, 13(2): 149-165.
     [7] Javed S. An Analytical Method to Calculate Borehole Fluid Temperatures for Time-scales from Minutes to Decades[J]. Ashrae Transactions. 2011, 117(2): 279-288.
     [8] Li M, Li P, Chan V, et al. Full-scale temperature response function (G-function) for heat transfer by borehole ground heat exchangers (GHEs) from sub-hour to decades[J]. Applied Energy. 2014, 136: 197-205.
     [9] Capozza A, Carli M D, Zarrella A. Investigations on the influence of aquifers on the ground temperature in ground-source heat pump operation[J]. Applied Energy. 2013, 107(107): 350-363.   
    [10] Philippe M, Bernier M, Marchio D. Validity ranges of three analytical solutions to heat transfer in the vicinity of single boreholes[J]. Geothermics. 2009, 38(4): 407-413.
    [11] Marcotte D, Pasquier P, Sheriff F, et al. The importance of axial effects for borehole design of geothermal heat-pump systems[J]. Renewable Energy. 2010, 35(4): 763-770.
    [12] Zeng H Y, Diao N R, Fang Z H. A finite line-source model for boreholes in geothermal heat exchangers[J]. Heat Transfer-Asian Research. 2002, 31(7): 558-567.
    [13] Li M, Lai A C K. New temperature response functions (G functions) for pile and borehole ground heat exchangers based on composite-medium line-source theory[J]. Energy. 2012, 38(1): 255-263.
    [14] Yang Y, Li M. Short-time performance of composite-medium line-source model for predicting responses of ground heat exchangers with single U-shaped tube[J]. International Journal of Thermal Sciences. 2014, 82(1): 130-137.
    [15] Li M, Lai A C K. Analytical model for short-time responses of ground heat exchangers with U-shaped tubes: Model development and validation[J]. Applied Energy. 2013, 104(2): 510-516.
    [16] Diao N, Li Q, Fang Z. Heat transfer in ground heat exchangers with groundwater advection[J]. International Journal of Thermal Sciences. 2004, 43(12): 1203-1211.
    [17] Sutton M G, Nutter D W, Couvillion R J. A Ground Resistance for Vertical Bore Heat Exchangers With Groundwater Flow[J]. Journal of Energy Resources Technology. 2003, 125(3): 183-189.
    [18] Molina-Giraldo N, Blum P, Zhu K, et al. A moving finite line source model to simulate borehole heat exchangers with groundwater advection[J]. International Journal of Thermal Sciences. 2011, 50(12): 2506-2513.
    [19] Lamarche L, Beauchamp B. A new contribution to the finite line-source model for geothermal boreholes[J]. Energy & Buildings. 2007, 39(2): 188-198.
    [20] Paul N D. The effect of grout thermal conductivity on vertical geothermal heat exchanger design and performance [D]. Vermillion, SD, USA: South Dakota University, 1996.
    [21] Claesson J, Hellström G. Multipole method to calculate borehole thermal resistances in a borehole heat exchanger[J]. Hvac & R Research. 2011, 17(6): 895-911.
    [22] Sharqawy M H, Mokheimer E M, Badr H M. Effective pipe-to-borehole thermal resistance for vertical ground heat exchangers[J]. Geothermics. 2009, 38(2): 271-277.

    備注：本文收錄于《建筑環境與能源》2018年10月刊總第15期（第21屆暖通空調制冷學術年會文集）。
              版權歸論文作者所有,任何形式轉載請聯系作者。